Obvody poloviční a úplné sčítačky
Obvody poloviční a úplné sčítačky jsou vysvětleny s jejich pravdivostními tabulkami v tomto článku. Je zde také uveden návrh úplné sčítačky pomocí obvodu poloviční sčítačky. Je také ukázán jednobitový obvod úplné sčítačky a vícebitové sčítání pomocí úplné sčítačky.
Předtím, než se pustíme do tohoto tématu, je velmi důležité vědět něco o logice Boolea a logických hradlech.
PODÍVEJTE SE : BOOLEAN LOGIC
PODÍVEJTE SE : LOGIC GATES
PODÍVEJTE SE : FLIP FLOPS
Co je to sčítačka?“
Sčítačka je druh kalkulátoru, který se používá ke sčítání dvou binárních čísel. Když říkám sčítačka, nemám na mysli tu s tlačítky, jedná se o obvod, který lze integrovat s mnoha dalšími obvody pro širokou škálu aplikací. Existují dva druhy sčítaček;
- Poloviční sčítačka
- Plná sčítačka
Poloviční sčítačka
Pomocí poloviční sčítačky můžeme navrhovat obvody, které jsou schopny provádět jednoduché sčítání pomocí logických hradel.
Nejprve se podívejme na sčítání jednotlivých bitů.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Tyto jsou nejméně možné kombinace jednotlivých bitů. Ale výsledek pro 1+1 je 10. Tento problém lze sice vyřešit pomocí hradla EXOR, ale pokud vám záleží na výstupu, je třeba výsledek součtu přepsat jako 2bitový výstup.
Takto lze výše uvedené rovnice zapsat jako
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Zde se výstup ‚1‘z ’10‘ stane carry-out. Výsledek je zobrazen v pravdivostní tabulce níže. ‚SUM‘ je normální výstup a ‚CARRY‘ je carry-out.
VÝSTUPY VÝSTUPY
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Z rovnice, je zřejmé, že tuto 1bitovou sčítačku lze snadno realizovat pomocí hradla EXOR pro výstup ‚SUM‘ a hradla AND pro přenos. Podívejte se na implementaci níže.
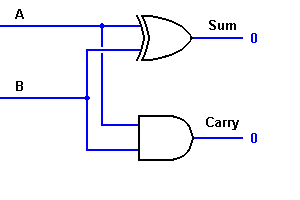
Pro složité sčítání mohou nastat případy, kdy je třeba sečíst dva 8bitové bajty. To lze provést pouze pomocí logiky plné sčítačky.
Plná sčítačka
Tento typ sčítačky je o něco náročnější na realizaci než poloviční sčítačka. Hlavní rozdíl mezi poloviční a plnou sčítačkou spočívá v tom, že plná sčítačka má tři vstupy a dva výstupy. První dva vstupy jsou A a B a třetí vstup je vstupní přenos označovaný jako CIN. Až bude navržena logika plné sčítačky, budeme jich moci zřetězit osm dohromady, abychom vytvořili bytovou sčítačku a kaskádovat přenosový bit z jedné sčítačky do druhé.
Výstupní přenos je označen jako COUT a normální výstup je označen jako S. Podívejte se na pravdivostní tabulku.
VSTUPY VÝSTUPY
A B CIN COUT S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1 1
Z výše uvedených pravd.tabulky, lze implementovat úplnou logiku sčítačky. Vidíme, že výstup S je EXOR mezi vstupem A a výstupem poloviční sčítačky SUM se vstupy B a CIN. Musíme si také uvědomit, že COUT bude pravdivý pouze v případě, že některý ze dvou vstupů ze tří bude HIGH.
Takto můžeme realizovat obvod úplné sčítačky pomocí dvou obvodů poloviční sčítačky. První bude poloviční sčítačka sloužit k sečtení A a B a vytvoření částečného součtu. Druhý logický obvod poloviční sčítačky lze použít k přičtení CIN k součtu vytvořenému první poloviční sčítačkou, abychom získali konečný výstup S. Pokud některá z logik poloviční sčítačky vytvoří přenos, bude na výstupu přenos. COUT tedy bude funkcí OR výstupů poloviční sčítačky Carry. Podívejte se na níže uvedenou implementaci obvodu úplné sčítačky.
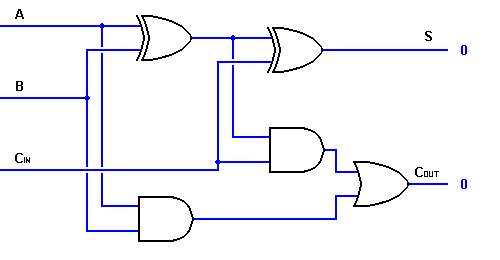
Přestože je s výše uvedenou logikou úplné sčítačky možná implementace větších logických schémat, pro znázornění operace se většinou používá jednodušší symbol. Níže je uvedeno jednodušší schéma znázorňující jednobitovou úplnou sčítačku.
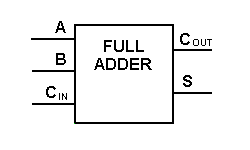
Pomocí tohoto typu symbolu můžeme sečíst dva bity, přičemž z dalšího nižšího řádu velikosti vezmeme přenos a do dalšího vyššího řádu velikosti pošleme přenos. V počítači musí být pro vícebitovou operaci každý bit reprezentován plnou sčítačkou a musí být sčítán současně. K sečtení dvou 8bitových čísel je tedy potřeba 8 plných sčítaček, které lze vytvořit kaskádováním dvou 4bitových bloků. Sčítání dvou 4bitových čísel je uvedeno níže.
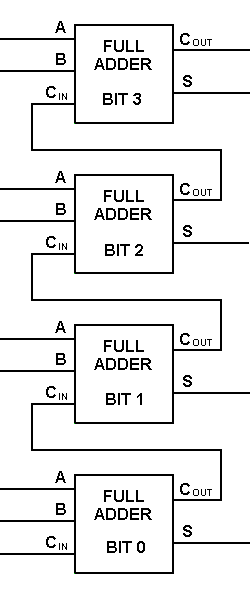
.