Čtvrťačka Alice se ptá: „Kolik úhlopříček má desetiúhelník?“
Skvělá otázka, Alice. Ale místo toho, abych ti na ni odpověděl, ti ukážu, jak na to můžeš přijít sama. A nejen to, ukážu ti, jak můžeš zjistit odpověď pro jakýkoli mnohoúhelník, i když má 20, 50 nebo 2000 stran!“
Připravena? Začněme jednoduchým příkladem. Vezmeme si mnohoúhelník, který má 8 stran (což se nazývá osmiúhelník), takto:
Nyní má tento mnohoúhelník, protože má osm stran, také osm vrcholů. Zdá se, že snažit se zjistit všechny úhlopříčky je poněkud zdrcující, proto se zaměříme jen na jeden vrchol. Kolik úhlopříček můžeš nakreslit v osmiúhelníku, které všechny začínají v jednom vrcholu?“
Odpověď na tuto otázku je pět. Podívejte se na následující diagram:

V tomto diagramu jsem zvolil úhlopříčku vlevo těsně pod horním vrcholem a nakreslil jsem úhlopříčky ke všem vrcholům, ke kterým mohu úhlopříčku nakreslit. Ke kterým úhlopříčkám nemohu úhlopříčky nakreslit? No, nemohu nakreslit úhlopříčku z vrcholu zpět k sobě a nemohu nakreslit úhlopříčky do dvou vrcholů vedle tohoto vrcholu (protože to by nebyly úhlopříčky, ale strany!).
Takže z tohoto vrcholu nemohu nakreslit úhlopříčky do tří vrcholů. Celkem osm vrcholů, po odečtení těch tří, ke kterým nemohu kreslit, zbývá pět. To je důležité si zapamatovat: od počtu vrcholů odečti 3 a máš počet úhlopříček, které můžeš nakreslit z libovolného vrcholu.
Ale to je jen jeden vrchol! Úhlopříčky přece můžete kreslit z libovolného vrcholu, ne? Jistě! A v našem osmiúhelníku je osm vrcholů, takže vezmeme počet úhlopříček na jeden vrchol a vynásobíme ho počtem vrcholů: 5 x 8 = 40.
Mohli byste být v pokušení myslet si, že to je naše odpověď, ale není. Proč ne? Protože jsme každou úhlopříčku počítali dvakrát! Každá úhlopříčka má dva vrcholy, takže jsme ji počítali z jednoho konce a počítali jsme ji i z druhého konce. Abychom tedy získali skutečný počet úhlopříček, musíme naši odpověď vydělit dvěma. 40 / 2 = 20. V osmiúhelníku je dvacet úhlopříček.
Zkusíme tuto úvahu na mnohoúhelníku, který má 2000 stran. Nebudu vám teď kreslit čtyřúhelník o 2000 stranách, budeme muset tuto úvahu vyřešit bez obrázku.
- Vyberte si vrchol. Kolik úhlopříček můžete z tohoto vrcholu nakreslit? Odpověď: 2000 – 3 = 1997.
- Kolik vrcholů celkem? Odpověď: 2000
- Kolik úhlopříček spočítáte ze všech vrcholů? Odpověď: Kolik je to7272? 1997 x 2000 = 3 994 000
- Oops! Každou úhlopříčku jsme počítali dvakrát! Jak se zbavíme duplicit? Odpověď: Jak vyřešíme duplicity? 3994000 / 2 = 1 997 000
Takže 2000-úhelník má 1 997 000 úhlopříček!
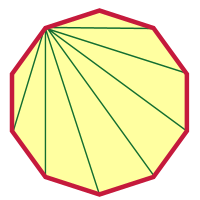
Po něčem tak šíleném, jako je 2000-úhelník, by se desetiúhelník neměl zdát tak složitý, ne? Já začnu a ty to můžeš dokončit odsud. Vybral jsem si vrchol a z něj jsem nakreslil úhlopříčky.
Kolik jich je? Dokázal jsi zjistit, kolik jich je, aniž by ses podíval na obrázek?“
Dokážeš to zjistit odsud? Doufám, že ano! Hodně štěstí, Alice.
Mimochodem, existuje vzorec, který můžeš použít; vypadá takto: D = n(n – 3)/2. Ale upřímně řečeno, neočekávám od svých studentů, že si ho zapamatují. Očekávám, že si zapamatují, jak to zde zdůvodníme. Pokud pochopíte logiku, je to dokonce lepší než mít vzorec!