Matematické modelování

Některé funkce jsou kusové. V této části se seznámíme s tím, jak definovat a vykreslovat grafy funkcí, které jsou v podstatě kolekcemi diskrétních částí. Příkladem něčeho takto definovaného může být návrh profilu automobilu, zjištění tarifu mobilního telefonu nebo výpočet sazby daně z příjmu. Například sazba daně závisí na vašem příjmu a je stejná pro různé příjmy, jak ukazuje následující tabulka:

Kusová funkce je funkce, ve které se k určení výstupu nad různými částmi oboru používá více vzorců.

Kusové funkce používáme k popisu situací, kdy se pravidlo nebo vztah mění s tím, jak vstupní hodnota překračuje určité „hranice“. Například v obchodě se často setkáváme se situacemi, pro které se cena za kus určitého zboží snižuje, jakmile počet objednaných kusů překročí určitou hodnotu. Dalším příkladem kusových funkcí v reálném světě jsou daňové závorky. Uvažujme například jednoduchý daňový systém, ve kterém jsou příjmy do 10 000 USD zdaněny sazbou 10 % a jakýkoli další příjem je zdaněn sazbou 20 %. Daň z celkového příjmu S by byla 0,1S, pokud S\le 10 000 USD, a 1000 + 0,2 (S – 10 000 USD), pokud S> 10 000 USD.

Vyhodnocení kusově definované funkce

V prvním příkladu si ukážeme, jak vyhodnotit kusově definovanou funkci. Všimněte si, jak je důležité věnovat pozornost doméně, aby bylo možné určit, který výraz použít k vyhodnocení vstupu.

V následujícím videu si ukážeme, jak vyhodnotit několik hodnot daných kusově definovanou funkcí.

V dalším příkladu si ukážeme, jak vyhodnotit funkci, která modeluje náklady na přenos dat pro telefonní společnost.

Analýza řešení

Funkci znázorňuje následující graf. Vidíme, kde se funkce při g=2 mění z konstanty na přímku s kladným sklonem. Grafy pro různé vzorce vyneseme na společnou sadu os, přičemž dbáme na to, aby každý vzorec byl aplikován na svůj správný obor.

C(g) = C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

. Zápis po částech definované funkce

V posledním příkladu si ukážeme, jak zapsat po částech definovanou funkci, která modeluje cenu prohlídky muzea s průvodcem.

Analýza řešení

Funkce je znázorněna na obrázku 21. V případě, že je n větší než 10, bude C=50. Grafem je úhlopříčka od n=0 do n=10 a poté konstanta. V tomto příkladu se oba vzorce shodují v bodě setkání, kde je n=10, ale ne všechny kusové funkce mají tuto vlastnost.

Na následujícím videu si ukážeme příklad zápisu kusově definované funkce daný scénářem.

Grafování kusových funkcí

V této části budeme vykreslovat kusové funkce. Níže vynesená funkce představuje náklady na přenos dat pro danou mobilní společnost. Vidíme, kde se funkce mění z konstanty na přímku s kladným sklonem při g=2. Při vykreslování kouskových funkcí je důležité se ujistit, že každý vzorec je aplikován na správnou oblast.C\left(g\right)=\begin{cases}{25} \text{ if }{ 0 }<{ g }<{ 2 }\\10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

V tomto případě je výstupem 25 pro jakýkoli vstup mezi 0 a 2. Pro hodnoty rovné nebo větší než 2 je výstup definován jako 10g+5.

Příklad

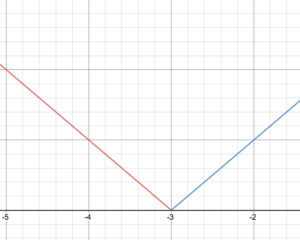
Nakreslete graf funkce.

Díky kusové definici f(x)=\begin{cases}-x – 3\text{ if }x < -3\\ x + 3\text{ if } x \ge -3\end{cases}
Nakreslete graf funkce f.
Uveďte obor a rozsah funkce.

Zobrazit odpověď

Nejprve nakreslete graf přímky f(x) = -x-3, přičemž vymažte část, kde je x větší než -3. V bodě (-3,0) umístěte otevřenou kružnici.

Na graf nyní umístěte přímku f(x) = x+3, která začíná v bodě (-3,0). Všimněte si, že pro tuto část grafu je bod (-3,0) zahrnut, takže můžete odstranit otevřenou kružnici.

Dva grafy se setkávají v bodě (-3,0)

Oblastí této funkce jsou všechna reálná čísla, protože bod (-3,0)není zahrnut jako koncový bod pro f(x) = -x-3, ale je zahrnut jako koncový bod pro f(x) = x+3. Všimněte si, že pro tuto část grafu je bod (-3,0) zahrnut.

Oblast této funkce začíná v bodě f(x)=0 a zahrnuje 0 a pokračuje do nekonečna, takže bychom ji zapsali jako x\ge0

V dalším příkladu vykreslíme graf po částech definované funkce, která modeluje náklady na dopravu pro internetového prodejce komiksů.

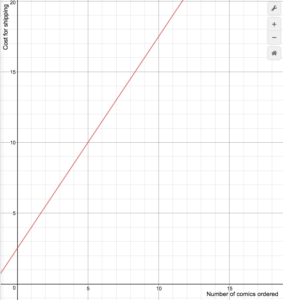
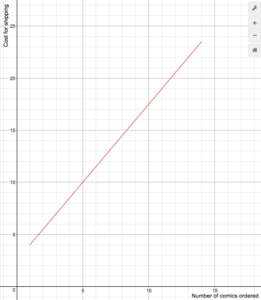
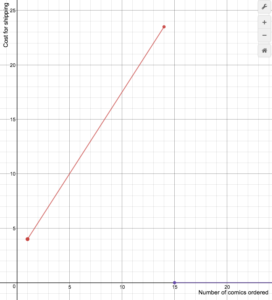
Příklad

Prodejce on-line komiksů účtuje náklady na dopravu podle následujícího vzorce

S(n)=\begin{případů}1,5n+2. V tomto vzorci jsou uvedeny náklady na dopravu.5\text{ if }1\le{n}\le14\0\text{ if }n\ge15\end{cases}

Nakreslete graf nákladové funkce.

Ukázat odpověď

Nejprve nakreslete přímku S(n)=1,5n+2,5. V grafu je znázorněno, že S(n)=1,5n+2,5. Můžeme použít transformace: jedná se o svislé protažení identity o faktor 1,5 a svislé posunutí o 2,5.

S(n)=1,5n+2. S(n)=1,5n+2. S(n)=1,5n+2.5

Nyní můžeme eliminovat části grafu, které nejsou v doméně na základě 1\le{n}\le14

S(n) = 1,5n+2,5 pro 1<=n<=14

Nakonec přidáme konstantní funkci S(n)=0 pro vstupy větší nebo rovné 15. Na závěr přidáme funkci S(n)=0 pro vstupy větší nebo rovné 10. Na konce grafu umístěte uzavřené tečky, které označují zařazení koncových bodů.

Na následujícím videu si ukážeme, jak vykreslit graf kusově definované funkce, která je lineární v obou oblastech.

Souhrn

• Kusově definovaná funkce je funkce, u které je k definování výstupu přes různé části domény použito více vzorců.
• Vyhodnocení kusově definované funkce znamená, že je třeba věnovat velkou pozornost správnému výrazu použitému pro daný vstup

Pro vykreslení grafu kusově definované funkce je třeba nejprve určit, kde je doména rozdělena. Na doméně vykreslete graf funkce pomocí nástrojů, jako je vykreslování bodů nebo transformace. Dejte pozor, abyste na koncových bodech každé domény použili otevřené nebo uzavřené kružnice podle toho, zda je koncový bod zahrnut

.