Předpoklad – Míry vzdálenosti v data miningu
V data miningu se mírou podobnosti rozumí vzdálenost s dimenzemi reprezentujícími vlastnosti datového objektu v souboru dat. Pokud je tato vzdálenost menší, bude existovat vysoký stupeň podobnosti, ale když je vzdálenost velká, bude existovat nízký stupeň podobnosti.
Některé z populárních měr podobnosti jsou –
- Euklidovská vzdálenost.
- Manhattanova vzdálenost.
- Jaccardova podobnost.
- Minkowského vzdálenost.
- Kosinová podobnost.
Kosinová podobnost je metrika, která pomáhá určit, jak jsou si datové objekty podobné bez ohledu na jejich velikost. Pomocí kosinové podobnosti můžeme měřit podobnost mezi dvěma větami v jazyce Python. V kosinové podobnosti jsou datové objekty v souboru dat považovány za vektor. Vzorec pro zjištění kosinové podobnosti mezi dvěma vektory je –
Cos(x, y) = x . y / ||x|| * ||y||
kde,
- x . y = součin (tečka) vektorů ‚x‘ a ‚y‘.
- ||x|| a ||y|| = délky dvou vektorů ‚x‘ a ‚y‘.
- ||x|| * ||y|| = křížový součin dvou vektorů ‚x‘ a ‚y‘.
Příklad :
Uvažujte příklad na zjištění podobnosti dvou vektorů – ‚x‘ a ‚y‘ pomocí kosinové podobnosti.
Vektor ‚x‘ má hodnoty, x = { 3, 2, 0, 5 }
Vektor ‚y‘ má hodnoty, y = { 1, 0, 0, 0 }
Vzorec pro výpočet kosinové podobnosti je : Cos(x, y) = x . y / ||x|| * ||y||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1∴ Cos(x, y) = 3 / (6.16 * 1) = 0.49
Nepodobnost mezi dvěma vektory ‚x‘ a ‚y‘ je dána vztahem –
∴ Dis(x, y) = 1 - Cos(x, y) = 1 - 0.49 = 0.51
- Kosinová podobnost mezi dvěma vektory se měří v ‚θ‘.
- Pokud θ = 0°, vektory ‚x‘ a ‚y‘ se překrývají, což dokazuje, že jsou podobné.
- Pokud θ = 90°, vektory ‚x‘ a ‚y‘ jsou nepodobné.
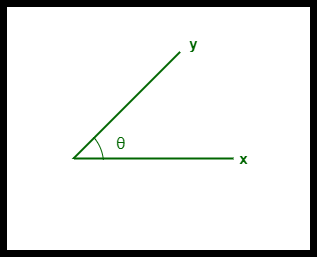
Kosinová podobnost dvou vektorů
Výhody :
- Kosinová podobnost je výhodná, protože i když jsou dva podobné datové objekty od sebe vzdáleny euklidovskou vzdáleností kvůli velikosti, stále mezi nimi může být menší úhel. Menší úhel znamená větší podobnost.
- Při vynesení do vícerozměrného prostoru kosinová podobnost zachycuje orientaci (úhel) datových objektů, nikoli jejich velikost.