VŠEOBECNÁ TÉMATA Z CHEMIE
Energie: Základní pojmy
Formy energie: Kinetická a potenciální.Práce a energie.Teplo a teplota.Elektrostatická potenciální energie.
Energie: kinetická a potenciální
Pojmy energie jsou pro fyzikální vědy základní. Zde si klademe za cíl stanovit některé první principy týkající se energie a představit některé formy, kterých energie nabývá a které mají pro chemii zvláštní význam. Především je často velmi užitečné definovat systém jako určitou část vesmíru, na které provádíme pozorování. Systém je tvořen objektem nebo souborem objektů a od zbytku vesmíru – kterému říkáme okolí – je odlišen skutečnou nebo pomyslnou hranicí.
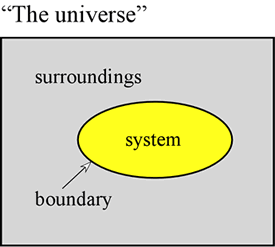
Příkladem soustavy je vzorek plynu držený v pevném objemu, například v kovovém válci – ten pro nás bude mít význam, až se budeme zabývat studiem obecných vlastností plynů. Dalšími příklady jsou vzorek plynu uvnitř balónku nebo spalovací směs ve válci s pístem. V obou těchto případech je soustava ohraničena fyzikální, ale pohyblivou hranicí, takže objem soustavy není pevný. Dalším příkladem, který budeme často uvažovat, je směs látek v roztoku, která prochází chemickou reakcí ve zkumavce nebo kádince. Terminologie zde zavedená má zvláštní význam při studiu toho, jak se energie projevuje v chemických systémech, které z velké části spadá pod termodynamiku.
V obecné chemii jsou systémy, které považujeme za relevantní, obvykle v klidu a gravitační účinky se zanedbávají. Často nás nejvíce zajímají systémy, v nichž probíhají chemické reakce, přičemž chemické složení systému se mění v čase. Přijměme však pro tuto chvíli širší pohled a použijme mechanické systémy, jako je kývající se kyvadlo nebo kutálející se a srážející se kulečníkové koule, které nám pomohou pochopit obecné principy týkající se energie.
O systému můžeme říci, že má energii dvěma různými způsoby, které nazýváme kinetická a potenciální energie. Kinetická energie je energie hmoty v pohybu. Fyzika poskytuje přesnou matematickou definici kinetické energie (KE), která je znázorněna v rovnici (vlevo dole).
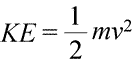
Kinetická energie objektu je zde znázorněna jako součin hmotnosti objektu (m) a čtverce jeho rychlosti (v), vynásobený také konstantou ½. Pokud se soustava skládá z více než jednoho objektu, je celková kinetická energie vyjádřitelná jako součet kinetických energií jednotlivých objektů.
Při této definici můžeme odvodit jednotky pro energii. Jednotkou energie v soustavě SI je joule (J), který je definován takto:
1 J = 1 kg-m-s-2
Potenciální energie je energie soustavy, kterou lze obvykle v nějaké formě přeměnit na kinetickou energii a která je schopna v určité míře vyprodukovat veličinu zvanou práce (o které pojednáváme dále). Jasným příkladem potenciální energie je cihla na římse budovy. Cihla má určité množství potenciální energie díky své výšce – poloze vzhledem ke gravitačnímu poli. Pokud do cihly šťouchneme tak, že spadne z římsy, samovolně se pohne ve směru nižší gravitační potenciální energie, a tím získá kinetickou energii. Jiným příkladem je elektrická potenciální energie baterie (která se vyjadřuje pomocí napětí). Když vytvoříme obvod s drátem a žárovkou, který spojuje dva póly baterie, rozdíl elektrických potenciálů mezi nimi způsobuje pohyb elektronů ve vodiči (kinetická energie), což vede k produkci tepla i světla.
Důležitou obecnou zásadou o energii je, že ji nelze ani vytvořit, ani zničit. To je známé jako zákon zachování energie. Kvantitativně to znamená, že v systému, jako je padající cihla nebo kyvadlo hodin, je součet kinetické a potenciální energie konstantní. To je do jisté míry abstrakce, protože ve skutečném kyvadle se část energie neustále ztrácí v důsledku tření a malé množství energie se musí kyvadlu přidávat, aby se udrželo v chodu (a hodiny fungovaly). Pokud však tuto „ztracenou“ energii (která se ve skutečnosti projevuje jako nárůst tepelné energie okolních molekul vzduchu) zohledníme pečlivým experimentálním měřením, zjistíme, že se energie skutečně vždy zachovává. Další výhrada je shrnuta ve slavné Einsteinově rovnici E = mc2, která vyjadřuje základní ekvivalenci hmoty a energie. Tuto ekvivalenci zohledňuje obecnější forma zákona zachování energie, kterou lze označit jako zákon zachování hmoty a energie. Vrátíme-li se k obecné chemii, takovéto vzájemné přeměny hmoty a energie nejsou typicky její doménou, zatímco studium jaderných reakcí a radioaktivity spadá do jaderné fyziky.
Uvažujeme-li o chemické reakci, při níž jsou chemické změny doprovázeny produkcí tepla, vyvstává otázka: Jak je to v tomto případě se zachováním energie? Odpověď zní, že existuje určitá forma potenciální energie, kterou můžeme nazvat chemickou potenciální energií (nebo prostě chemickým potenciálem), o níž si můžeme myslet, že se nachází v molekulárním složení reaktantů. Tato potenciální energie se pak přeměňuje na energii ve formě tepla, ale ukazuje se, že čisté množství přítomné energie zůstává konstantní, jakmile jsme schopni definovat a měřit produkci tepla. Každodenní příklad toho, co nyní můžeme chápat jako chemickou potenciální energii, uvádí benzínový motor, v němž směs benzínu a kyslíku disponuje latentní formou energie. Tato latentní energie ve směsi benzinu a kyslíku se vynakládá na výrobu kinetické energie automobilu.
Práce a energie
Práce je dalším pojmem, který ve fyzice připouští přesnou definici. Zákony mechaniky lze navíc propojit s energií pomocí věty o práci a energii. Kopnutí fotbalového míče nebo libovolný počet podobných příkladů ilustruje myšlenku, že kinetickou energii objektu lze zvýšit působením síly. Větu o práci a energii, která je zobecněním této myšlenky, lze vyjádřit zhruba takto: Změna energie, kterou má objekt, se rovná velikosti síly, která na něj působí, vynásobené vzdáleností, v níž síla působí.
Změna energie, k níž dochází v systému v důsledku práce, může být z hlediska systému kladná nebo záporná. Práci může vykonat systém, nebo na systém může působit práce vykonaná okolím. Pokud je práce vykonávána systémem, ztrácí systém energii ve prospěch okolí. Pokud je na systému vykonána práce, energie systému se zvyšuje. Například když jiskra, která spustí spalovací směs ve válci s pohyblivým pístem, způsobí rychlou expanzi systému a tato expanze je mechanicky spojena s pohybem tyče v okolí, systém válce koná práci na okolí, a tím ztrácí energii. To je samozřejmě součástí toho, jak spalovací motor přeměňuje chemickou potenciální energii na kinetickou energii pohybujícího se automobilu.
Jeden z důsledků věty o práci a energii se týká jednotek, totiž že práci lze měřit ve stejných jednotkách jako energii. Protože druhý Newtonův zákon je síla = hmotnost × zrychlení, newton (N), jednotka SI pro sílu, je odvozen jako M × L × T -2, a tedy 1 N = 1 kg m s-2. Síla krát vzdálenost má hodnoty M × L2 × T -2, a proto je jednotka SI pro energii, joule (J), definována jako 1 J = 1 kg m2 s-2. Na tomto místě byste si měli sami ověřit, že rovnice pro kinetickou energii zahrnuje stejnou kombinaci základních veličin hmotnost (M), délka (nebo vzdálenost, L) , a čas (T).
Teplo a teplota
Slova teplo a teplota používáme poměrně často a často hovoříme o teple jako o formě energie. Všichni máme intuitivní pocit, co to je, ale zde o nich chceme přemýšlet více vědecky a dát jim formálnější definice, pokud je to možné. To je nutná předehra ke kvantifikaci energie odpovídající teplu a odtud k měřením, která ověří zákon zachování energie. Zjistíme, že tepelnou energii systému lze přirovnat k celkové kinetické energii (jak je definována výše) atomů a molekul, které jej tvoří. Teplota objektu nebo systému je vlastně mírou průměrné kinetické energie atomů a/nebo molekul, z nichž se skládá. (Pozn. teplota není přesně rovna průměrné kinetické energii molekul, ale je jí přímo úměrná. Další podrobnosti naleznete na webové stránce o kinetické teorii molekul.)
Jedním ze způsobů, jak si představit, co máme na mysli pod pojmy teplo a teplota a jaký je mezi nimi rozdíl, je uvažovat o analogii s kulečníkovou koulí. V některých jednoduchých souvislostech je chování kulečníkových koulí vhodným modelem pro soubor atomů nebo molekul, například ve vzorku plynu. Stejně jako kulečníkové koule, které byly právě zasaženy rychle se pohybující kulečníkovou koulí, se molekuly plynu pohybují všude kolem, odrážejí se navzájem a od stěn nádoby, v níž jsou uloženy. Celková kinetická energie kulečníkových koulí, která je právě součtem kinetických energií jednotlivých koulí, je analogická tepelné energii vzorku molekul plynu. Při „přestávce“ na začátku kulečníkové hry se počáteční kinetická energie tágové koule rozdělí mezi všechny koule na stole. Některé se pohybují poměrně rychle a jiné ne tak rychle, ale analogicky k „teplu“ nebo „tepelné energii“ je pro soustavu kulečníkových koulí právě součet těchto kinetických energií. Na druhé straně by teplota soustavy kulečníkových koulí byla úměrná průměrné kinetické energii souboru koulí.
Elektrostatická potenciální energie
Zákon elektrostatické přitažlivosti a odpuzování neboli Coulombův zákon popisuje sílu, kterou působí na nabitý objekt v důsledku přítomnosti jiného nabitého objektu. Sílu lze nejsnáze vypočítat, pokud lze náboje považovat za velmi malé bodové náboje. Velikost síly, kterou nabitý objekt „cítí“, je úměrná součinu nábojů (jednotka SI pro elektrický náboj je Coulomb, C) a nepřímo úměrná čtverci vzdálenosti mezi náboji (r na obrázku vpravo). Síla je přitažlivá (podobně jako gravitace a na obrázku je označena šipkami směřujícími dovnitř), pokud mají náboje opačné znaménko, a odpudivá, pokud mají náboje stejné znaménko.
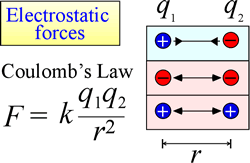
Když síly (jako jsou elektrostatické, magnetické a gravitační síly) mohou působit na dálku (prostorem, bez mechanického kontaktu), říká se, že objekty podléhající těmto silám se nacházejí v poli potenciální energie. Výše jsme hovořili o gravitační potenciální energii a podobně v případě elektrostatických sil bude mít nabitý objekt elektrostatickou potenciální energii díky tomu, že se nachází v elektrickém poli. Takové pole existuje v blízkosti jakéhokoli jiného náboje nebo nábojů.
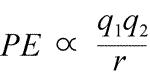
Rovnice pro elektrostatickou potenciální energii: PE je úměrná nábojům q1 a q2 a nepřímo úměrná separační vzdálenosti, r. Tvar funkce potenciální energie matematicky vyplývá z vyjádření síly, Coulombova zákona.
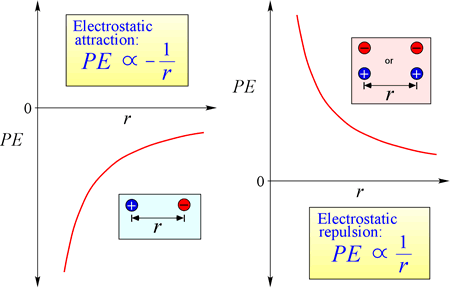
Vzhledem k opačným znaménkům přitahujících se nábojů je potenciální energie vždy záporná a čím více se náboje přibližují, tím je potenciální energie zápornější – tj. nižší. Jak se separační vzdálenost r blíží nule, potenciální energie se stává nekonečně zápornou. Pro náboje stejného znaménka je energie odpuzování vždy kladná a s blížící se separační vzdáleností, r, se stává nekonečně kladnou.
Elektrostatická potenciální energie je důležitým faktorem v chemii. Pochopení podstaty atomu, chemické vazby a mezimolekulárních sil je naprosto závislé na zohlednění vlivu interakcí náboj-náboj, které přispívají k energii systému.
Důležité jednotky
Energie (jednotka SI) 1 joule = 1 J = 1 kg-m-s-2
Elementární náboj, e = 1,60218 × 10-19 C (coulomb, C)
Faradayova konstanta: F = NAe = 9,64853 × 104 C-mol-1
Elektrický potenciál: volty, V 1 V = 1 J C-1
.