Nestává se často, aby se matematická rovnice dostala do celostátního tisku, tím méně do populárního rádia nebo, což je nejpřekvapivější, aby se stala předmětem debaty v britském parlamentu. Tím vším se však v roce 2003 stala stará dobrá kvadratická rovnice, o které jsme se všichni učili ve škole.
Kde začneme

Vše začalo na zasedání Národního odborového svazu učitelů. Kvadratická rovnice byla vztyčena před národem jako příklad krutého mučení, které matematici způsobují nebohým nic netušícím školákům. Kvadratická rovnice, zaujatá tímto obviněním, přijala hlavní roli v hlavním vysílacím čase rozhlasu, kde ji zpovídal impozantní tazatel zvyklý spíše na premiéra. (Londýnské) Timesy využily prostor ve svém sloupku Leader, který je obvykle vyhrazen pro závažné diskuse o morálním zdraví moderního světa, aby prohlásily, že kvadratická rovnice je k ničemu, matematika je k ničemu a že ji stejně nikdo nechce studovat, tak proč se namáhat. V obavě, aby nebezpečná přiznání kvadratické rovnice nezůstala nezpochybněna, se o životně důležitém významu rovnice pro přežití Spojeného království diskutovalo (možná vás potěší, že bylo zaujato kladné stanovisko) v britské Dolní sněmovně.
Kde by to všechno skončilo? Byla kvadratická rovnice skutečně mrtvá? Zajímalo to vůbec někoho? Jsou matematici opravdu zlá monstra, která chtějí kvadratickou rovnici vnutit jen mladé generaci jako prostředek ke zkažení její nesmrtelné duše?“
Možná ano, ale kvadratická rovnice za to ve skutečnosti nemůže. Kvadratická rovnice totiž sehrála klíčovou roli nejen v celé lidské civilizaci, jak ji známe, ale i v možném odhalení jiných mimozemských civilizací a dokonce i v tak životně důležitých moderních činnostech, jako je sledování satelitní televize. Co jiného, kromě povahy božského zjevení, by mohlo mít takový vliv na život, jak ho známe? Vskutku, ve velmi reálném smyslu vám kvadratické rovnice mohou zachránit život.
Babylóňané
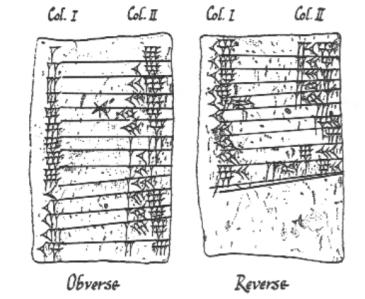
Babylonské klínopisné tabulky se záznamem devíti časových tabulek
Vše začalo kolem roku 3000 př. n. l. u Babyloňanů. Byli jednou z prvních civilizací na světě a přišli s několika skvělými nápady, jako je zemědělství, zavlažování a písmo. Zakreslovali dráhy Slunce, Měsíce a planet a zaznamenávali je na hliněné tabulky (které si dodnes můžete prohlédnout v Britském muzeu). Babyloňanům vděčíme za moderní představy o úhlu, včetně způsobu, jakým je kruh rozdělen na 360 stupňů (díky malé chybě ve výpočtu, jeden na den). Babylóňanům vděčíme také za poněkud méně příjemný vynález (obávaného) berňáku. A to byl jeden z důvodů, proč Babylóňané potřebovali řešit kvadratické rovnice.
Předpokládejme, že jste babylonský zemědělec. Někde na svém statku máte čtvercové pole, na kterém pěstujete nějakou plodinu. Jaké množství plodiny můžete na tomto poli vypěstovat? Zdvojnásobte délku každé strany pole a zjistíte, že můžete vypěstovat čtyřikrát více plodiny než dříve. Důvodem je to, že množství plodiny, které můžete vypěstovat, je úměrné ploše pole, která je zase úměrná čtverci délky strany. Matematicky řečeno, je-li  délka strany pole,
délka strany pole, 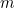 je množství plodiny, které můžete vypěstovat na čtvercovém poli o délce strany 1, a
je množství plodiny, které můžete vypěstovat na čtvercovém poli o délce strany 1, a  je množství plodiny, které můžete vypěstovat, pak
je množství plodiny, které můžete vypěstovat, pak
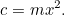 |
To je naše první kvadratická rovnice, nahá a blikající ve slunečním světle. Kvadratické rovnice a plochy spolu souvisejí jako sourozenci v jedné rodině. V tuto chvíli však nemusíme nic řešit – tedy dokud nepřijde daňový úředník! Vesele řekne farmáři: „Chci, abys mi dal plodiny na zaplacení daní z tvého hospodářství.“ A pak se na něj podívá. Zemědělec má nyní dilema: jak velké pole potřebuje, aby vypěstoval takové množství obilí? Na tuto otázku můžeme odpovědět snadno, ve skutečnosti
plodiny na zaplacení daní z tvého hospodářství.“ A pak se na něj podívá. Zemědělec má nyní dilema: jak velké pole potřebuje, aby vypěstoval takové množství obilí? Na tuto otázku můžeme odpovědět snadno, ve skutečnosti
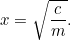 |
Zjistit odmocniny pomocí kalkulačky je pro nás snadné, ale pro Babyloňany to byl větší problém. Vyvinuli totiž metodu postupného přibližování k odpovědi, která je totožná s algoritmem (nazývaným Newtonova-Raphsonova metoda), který používají moderní počítače k řešení mnohem těžších problémů, než jsou kvadratické rovnice.
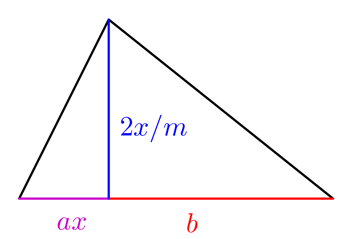
Ne všechna pole jsou nyní kvadratická. Předpokládejme nyní, že farmář má pole zvláštnějšího tvaru se dvěma trojúhelníkovými výsečemi, jak je znázorněno vpravo.
Při vhodných hodnotách  a
a 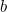 je množství plodin, které může farmář na tomto poli vypěstovat, dáno vztahem
je množství plodin, které může farmář na tomto poli vypěstovat, dáno vztahem
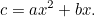 |
To se mnohem více podobá kvadratické rovnici, na kterou jsme zvyklí, a i pod zlým okem daňového úředníka je mnohem těžší ji vyřešit. Přesto Babylóňané opět přišli s odpovědí. Nejprve vydělíme  a dostaneme
a dostaneme
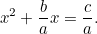 |
Nyní doplníme čtverec pomocí toho, že
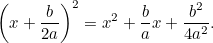 |
Spojením s původní rovnicí dostaneme
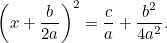 |
To je nyní rovnice, kterou můžeme řešit odmocňováním. Výsledkem je známý „vzorec 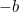 „:
„:
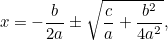 |
, který lze přepsat takto
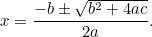 |
(Ve vzorci se obvykle uvádí „-4ac“, protože kvadratická rovnice se obvykle zapisuje spíše ve tvaru „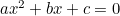 „.)
„.)
To, že odmocňování může dát kladnou nebo zápornou odpověď, vede k pozoruhodnému výsledku, že kvadratická rovnice má dvě řešení. Tolik k tomu, že matematické hádanky mají pouze jedno řešení!
Tady výuka kvadratických rovnic často končí. Dostali jsme se k onomu objektu, který milují všichni novináři, když dělají rozhovory s matematiky – ke vzorci. Lze vymyslet nekonečné množství otázek, které spočívají v dosazení hodnot 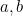 a
a  do vzorce, čímž získáme (dvě) odpovědi. Ale o tom matematika vůbec není. Nalezení vzorce je pouze prvním krokem na dlouhé cestě. Musíme se ptát, co vzorec znamená; co nám říká o vesmíru; má to, že máme vzorec, skutečný význam? Podívejme se nyní, kam nás tento vzorec zavede.
do vzorce, čímž získáme (dvě) odpovědi. Ale o tom matematika vůbec není. Nalezení vzorce je pouze prvním krokem na dlouhé cestě. Musíme se ptát, co vzorec znamená; co nám říká o vesmíru; má to, že máme vzorec, skutečný význam? Podívejme se nyní, kam nás tento vzorec zavede.
Překvapení pro Řeky, trocha matematického origami a smysl pro proporce
Nyní se přeneseme o 1000 let dopředu ke starým Řekům a podíváme se, co vytvořili z kvadratických rovnic. Řekové byli vynikající matematici a objevili velkou část matematiky, kterou používáme dodnes. Jednou z rovnic, která je zajímala, bylo řešení (jednoduché) kvadratické rovnice
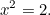 |

Věděli, že tato rovnice má řešení. Ve skutečnosti je to délka přepony pravoúhlého trojúhelníku, který měl strany délky jedna.
Z Pythagorovy věty vyplývá, že pokud je pravoúhlýúhlový trojúhelník kratší strany  a
a  a přeponu
a přeponu  , pak
, pak
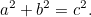 |
Dosazení 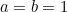 a
a  pak
pak 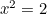 . Tedy
. Tedy 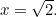
Co je tedy v tomto případě  ? Nebo, abychom položili otázku, kterou si kladli Řekové, co je to za číslo? Důvod, proč na tom záleželo, spočíval v řeckém smyslu pro proporce. Věřili, že všechna čísla jsou ve vzájemném poměru. Přesněji řečeno to znamenalo, že všechna čísla jsou zlomky tvaru
? Nebo, abychom položili otázku, kterou si kladli Řekové, co je to za číslo? Důvod, proč na tom záleželo, spočíval v řeckém smyslu pro proporce. Věřili, že všechna čísla jsou ve vzájemném poměru. Přesněji řečeno to znamenalo, že všechna čísla jsou zlomky tvaru 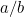 , kde
, kde  a
a  jsou celá čísla. Čísla jako 1/2, 3/4 a 355/113 jsou příklady zlomků. Bylo přirozené očekávat, že
jsou celá čísla. Čísla jako 1/2, 3/4 a 355/113 jsou příklady zlomků. Bylo přirozené očekávat, že  je také zlomek. Obrovským překvapením bylo, že tomu tak není. Ve skutečnosti
je také zlomek. Obrovským překvapením bylo, že tomu tak není. Ve skutečnosti
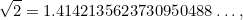 |
, kde tečky  znamenají, že desetinné rozšíření
znamenají, že desetinné rozšíření  pokračuje do nekonečna bez jakéhokoli rozeznatelného vzoru. (S touto situací se ještě setkáme později, až se budeme učit o chaosu.)
pokračuje do nekonečna bez jakéhokoli rozeznatelného vzoru. (S touto situací se ještě setkáme později, až se budeme učit o chaosu.)
 bylo první iracionální číslo (tj. číslo, které není zlomkem ani racionálním číslem), které bylo jako takové uznáno. Mezi další příklady patří
bylo první iracionální číslo (tj. číslo, které není zlomkem ani racionálním číslem), které bylo jako takové uznáno. Mezi další příklady patří 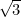 ,
,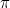 ,
,  a vlastně „většina“ čísel. Trvalo až do 19. století, než jsme o těchto číslech začali dobře uvažovat. Objev, že
a vlastně „většina“ čísel. Trvalo až do 19. století, než jsme o těchto číslech začali dobře uvažovat. Objev, že  není racionální číslo, způsobil jak velké vzrušení (v důsledku toho bylo obětováno 100 volů), tak velký šok, přičemž objevitel musel spáchat sebevraždu. (Budiž to strašlivým varováním pro matematicky nadšené!) V tomto okamžiku se Řekové vzdali algebry a přešli ke geometrii.
není racionální číslo, způsobil jak velké vzrušení (v důsledku toho bylo obětováno 100 volů), tak velký šok, přičemž objevitel musel spáchat sebevraždu. (Budiž to strašlivým varováním pro matematicky nadšené!) V tomto okamžiku se Řekové vzdali algebry a přešli ke geometrii.
S číslem  se zdaleka nejedná o obskurní číslo, setkáváme se s ním pravidelně: kdykoli použijeme list papíru A4. V Evropě se velikost papíru měří ve velikostech A, přičemž A0 je největší s plochou
se zdaleka nejedná o obskurní číslo, setkáváme se s ním pravidelně: kdykoli použijeme list papíru A4. V Evropě se velikost papíru měří ve velikostech A, přičemž A0 je největší s plochou 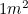 . Velikosti A mají mezi sebou zvláštní vztah. Pokud nyní provedeme trochu origami, vezmeme list papíru A1 a přeložíme jej na polovinu (podél nejdelší strany), získáme papír A2. Dalším přeložením na polovinu získáme papír A3, dalším přeložením na polovinu získáme papír A4 atd. Papír je však navržen tak, aby proporce každé z velikostí A byla stejná – to znamená, že každý kus papíru má stejný tvar.
. Velikosti A mají mezi sebou zvláštní vztah. Pokud nyní provedeme trochu origami, vezmeme list papíru A1 a přeložíme jej na polovinu (podél nejdelší strany), získáme papír A2. Dalším přeložením na polovinu získáme papír A3, dalším přeložením na polovinu získáme papír A4 atd. Papír je však navržen tak, aby proporce každé z velikostí A byla stejná – to znamená, že každý kus papíru má stejný tvar.
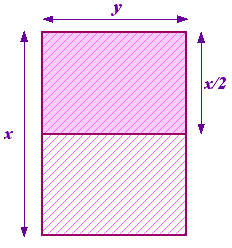
Můžeme si položit otázku, o jakou proporci se jedná. Začněte s kusem papíru se stranami x a y, přičemž x je nejdelší strana. Nyní jej rozdělíme na dvě části a získáme další kus papíru se stranami y a x/2, přičemž nyní je y nejdelší stranou. To je znázorněno na obrázku vpravo.
Poměry prvního kusu papíru jsou 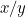 a poměry druhého kusu papíru jsou
a poměry druhého kusu papíru jsou 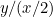 nebo
nebo 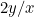 . Chceme, aby se tyto dva poměry rovnaly. To znamená, že
. Chceme, aby se tyto dva poměry rovnaly. To znamená, že
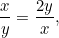 |
neboli
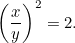 |
Další kvadratická rovnice! Naštěstí je to ta, se kterou jsme se již setkali. Při jejím řešení zjistíme, že
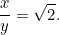 |
Tento výsledek si snadno ověříte. Stačí vzít list papíru formátu A4 (nebo A3 či A5) a změřit strany. Můžeme také zjistit velikost jednotlivých listů. Plocha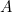 listu papíru A0 je dána vztahem
listu papíru A0 je dána vztahem
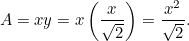 |
Víme však, že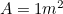 , takže máme další kvadratickou rovnici pro nejdelší stranu
, takže máme další kvadratickou rovnici pro nejdelší stranu listu A0, danou vztahem
listu A0, danou vztahem
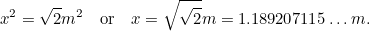 |
To znamená, že nejdelší strana A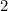 je dána vztahem
je dána vztahem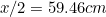 (proč?) a délku A
(proč?) a délku A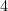
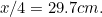 . Zkontrolujte si je na vlastních listech papíru.
. Zkontrolujte si je na vlastních listech papíru.
Papír používaný ve Spojených státech, nazývaný foolscap, má jiný poměr. Abychom zjistili proč, vrátíme se k Řekům a další kvadratické rovnici. Poté, co způsobila takový zármutek, se kvadratická rovnice vykoupila při hledání dokonalých proporcí: hledání, které pokračuje dodnes při navrhování filmových kulis a lze ho pozorovat v mnoha aspektech přírody.
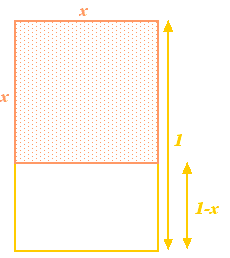
Začněme s obdélníkem a pak z něj odstraňme čtverec o stejné délce strany, jako je nejkratší strana obdélníku. Má-li nejdelší strana obdélníku délku 1 a nejkratší strana délku  , pak má čtverec strany délky
, pak má čtverec strany délky  . Jeho odebráním z obdélníku získáme menší obdélník s nejdelší stranou
. Jeho odebráním z obdélníku získáme menší obdélník s nejdelší stranou  a nejmenší stranou
a nejmenší stranou 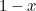 . Zatím je to tak abstraktní. Řekové však věřili, že obdélník, který má nejestetičtější proporce (tzv. zlatý obdélník), je ten, u něhož mají výše sestrojené velké a malé obdélníky stejné proporce. Aby to bylo možné, musíme mít
. Zatím je to tak abstraktní. Řekové však věřili, že obdélník, který má nejestetičtější proporce (tzv. zlatý obdélník), je ten, u něhož mají výše sestrojené velké a malé obdélníky stejné proporce. Aby to bylo možné, musíme mít
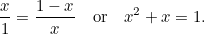 |
To je další kvadratická rovnice: velmi důležitá, která se objevuje v nejrůznějších aplikacích. Má (kladné) řešení
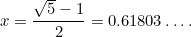 |
Číslo  se nazývá zlatý řez a často se označuje řeckým písmenem
se nazývá zlatý řez a často se označuje řeckým písmenem 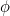 .
.

Zlatý obdélník můžeme vidět ve tvaru oken, zejména na georgiánských domech. Nověji se se zlatým řezem můžeme setkat také jako s „dokonalým tvarem“ fotografií a filmových snímků. Kvadratická rovnice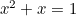 se objevuje také při studiu populací králíků a ve vzoru, v němž jsou uspořádána semena slunečnic a listy na stoncích rostlin. To vše souvisí se zlatým řezem prostřednictvím Fibonacciho posloupnosti, která je dána
se objevuje také při studiu populací králíků a ve vzoru, v němž jsou uspořádána semena slunečnic a listy na stoncích rostlin. To vše souvisí se zlatým řezem prostřednictvím Fibonacciho posloupnosti, která je dána
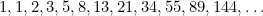 |

Slunečnicová semena, uspořádaná pomocí Fibonacciho čísel |
Parthenon, ztělesňující zlatý řez |
V této posloupnosti je každý člen součtem dvou předchozích. Fibonacci ji objevil v 15. století ve snaze předpovědět budoucí populaci králíků. Pokud vezmete poměr každého členu k členu následujícímu, dostanete posloupnost čísel
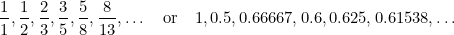 |
a tato čísla se stále více blíží (hádáte správně) zlatému řezu 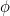 .
.
Nalezením obou kořenů výše uvedené kvadratické rovnice můžeme vlastně najít vzorec pro n-tý člen Fibonacciho posloupnosti. Je-li 
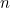 takové číslo s
takové číslo s 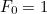 a
a 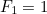 , pak
, pak  je dáno vzorcem
je dáno vzorcem
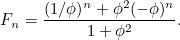 |
Kóniky spojují kvadratické rovnice s hvězdami

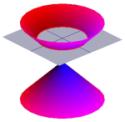
Řekové se také velmi zajímali o tvar kuželů. Obrázek vlevo ukazuje typický kužel.
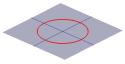
Polovinu kužele si lze představit jako rozptyl světla vycházejícího z pochodně. Svítíte-li nyní baterkou na rovný povrch, například na stěnu, pak při pohybu baterky uvidíte různé tvary. Tyto útvary se nazývají kuželosečky a jsou to křivky, které získáte, pokud provedete řez kuželem pod různými úhly. Právě tyto křivky studovali Řekové a zjistili, že existují v podstatě čtyři typy kuželoseček. Vezmeme-li vodorovný řez kuželosečkou, dostaneme kružnici. Při řezu pod malým úhlem k vodorovné rovině získáme elipsu. Pokud vezmeme svislý řez, dostaneme hyperbolu, a pokud vezmeme řez rovnoběžný s jednou stranou kužele, dostaneme parabolu. Tyto křivky jsou znázorněny níže.
 |
 |
 |
 |
 |
 |
 |
 |

Křížek-průřez kužele může být kružnice …. |

… elipsa … |
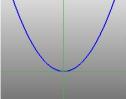
… parabola … |
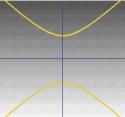
…. nebo hyperbola. |
Konické úsečky vstupují do našeho příběhu, protože každá z nich je popsána kvadratickou rovnicí. Konkrétně pokud 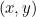 představuje bod na každé křivce, pak kvadratická rovnice spojuje
představuje bod na každé křivce, pak kvadratická rovnice spojuje  a
a 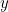 . Máme tedy:
. Máme tedy:
Kruh: 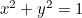 ;
;
Elipsa: 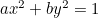 ;
;
Hiperbola: 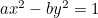 ;
;
Parabola: 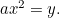
Tyto křivky byly známy a studovány již od dob Řeků, ale kromě kružnice se nezdálo, že by měly nějaké praktické využití. Jak však uvidíme v příštím čísle Plusu, souvislost mezi kvadratickými rovnicemi a kuželosečkami spolu s mocnou šťastnou náhodou vedla k pochopení fungování vesmíru a v 16. století nastal čas, kdy kuželosečky změnily svět.
O autorech
Chris Budd je profesorem aplikované matematiky na katedře matematických věd na univerzitě v Bathu a vedoucím katedry matematiky na Královském institutu v Londýně.
Chris Sangwin je zaměstnancem školy matematiky a statistiky na univerzitě v Birminghamu. Je výzkumným pracovníkem centra Learning and Teaching Support Network pro matematiku, statistiku a operační výzkum.
Nedávno napsal populární matematickou knihu Mathematics Galore! vydanou nakladatelstvím Oxford University Press.
Tento článek byl částečně inspirován pozoruhodnou debatou v britské Dolní sněmovně na téma kvadratických rovnic. Záznam této debaty lze nalézt v Hansardu, Dolní sněmovna Spojeného království, 26. června 2003, sloupce 1259-1269, 2003, který je dostupný online na webových stránkách House of Commons Hansard Debate.