Různé typy regulátorů se používají ke zlepšení výkonu řídicích systémů. V této kapitole se budeme zabývat základními regulátory, jako jsou proporcionální, derivační a integrální regulátory.
Proporcionální regulátor
Proporcionální regulátor vytváří výstup, který je úměrný chybovému signálu.
$$u(t) \propto e(t) $$
$$Pravá šipka u(t)=K_P e(t)$$
Aplikujte Laplaceovu transformaci na obě strany -.
$$U(s)=K_P E(s)$$
$\frac{U(s)}{E(s)}=K_P$$
Tedy, přenosová funkce proporcionálního regulátoru je $K_P$.
Kde,
U(s) je Laplaceova transformace akčního signálu u(t)
E(s) je Laplaceova transformace chybového signálu e(t)
KP je konstanta proporcionality
Blokové schéma systému řízení s jednotnou zápornou zpětnou vazbou v uzavřené smyčce spolu s proporcionálním regulátorem je znázorněno na následujícím obrázku.
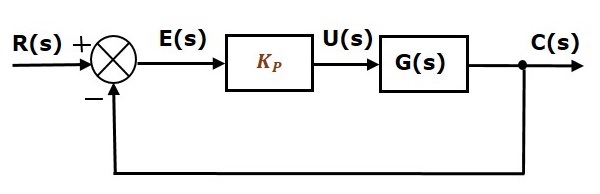
Proporcionální regulátor se používá ke změně přechodové odezvy podle požadavku.
Derivační regulátor
Derivační regulátor vytváří výstup, který je derivací chybového signálu.
$$u(t)=K_D \frac{\text{d}e(t)}{\text{d}t}$
Použijeme Laplaceovu transformaci na obě strany.
$$U(s)=K_D sE(s)$$
$$\frac{U(s)}{E(s)}=K_D s$$
Přenosová funkce derivačního regulátoru je tedy $K_D s$.
Kde $K_D$ je derivační konstanta.
Blokové schéma uzavřeného řídicího systému s jednotnou zápornou zpětnou vazbou spolu s derivačním regulátorem je znázorněno na následujícím obrázku.
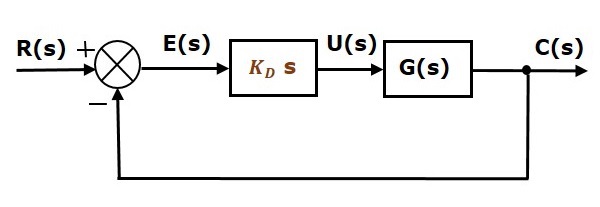
Derivační regulátor se používá k tomu, aby se z nestabilního řídicího systému stal stabilní.
Integrální regulátor
Integrální regulátor vytváří výstup, který je integrálem chybového signálu.
$$u(t)=K_I \int e(t) dt$$
Použijeme Laplaceovu transformaci na obě strany –
$$U(s)=\frac{K_I E(s)}{s}$$
$\frac{U(s)}{E(s)}=\frac{K_I}{s}$$
Tedy, přenosová funkce integrálního regulátoru je $\frac{K_I}{s}$.
Kde $K_I$ je integrální konstanta.
Blokové schéma systému řízení s jednotnou zápornou zpětnou vazbou v uzavřené smyčce spolu s integrálním regulátorem je znázorněno na následujícím obrázku.
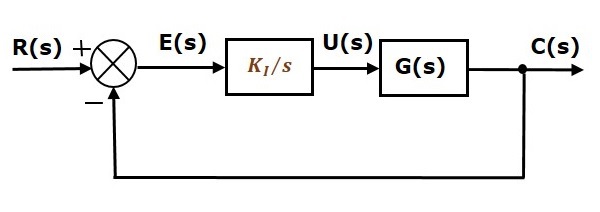
Integrální regulátor se používá ke snížení chyby ustáleného stavu.
Probírejme nyní kombinaci základních regulátorů.
Proporcionálně derivační (PD) regulátor
Proporcionálně derivační regulátor vytváří výstup, který je kombinací výstupů proporcionálního a derivačního regulátoru.
$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}$
Použijeme Laplaceovu transformaci na obě strany -.
$$U(s)=(K_P+K_D s)E(s)$$
$$\frac{U(s)}{E(s)}=K_P+K_D s$$
Tedy, přenosová funkce proporcionálního derivačního regulátoru je $K_P + K_D s$.
Blokové schéma systému řízení s jednotnou zápornou zpětnou vazbou v uzavřené smyčce spolu s proporcionálně derivačním regulátorem je znázorněno na následujícím obrázku.
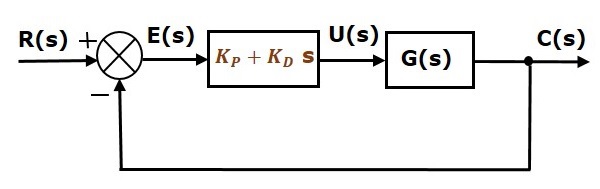
Proporcionálně derivační regulátor se používá ke zlepšení stability řídicího systému bez vlivu na chybu ustáleného stavu.
Proporcionálně integrální (PI) regulátor
Proporcionálně integrální regulátor vytváří výstup, který je kombinací výstupů proporcionálního a integrálního regulátoru.
$$u(t)=K_P e(t)+K_I \int e(t) dt$$
Použijeme Laplaceovu transformaci na obě strany -.
$$U(s)=\levá(K_P+\frac{K_I}{s} \pravá )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$
Tedy, přenosová funkce proporcionálního integrálního regulátoru je $K_P + \frac{K_I} {s}$.
Blokové schéma systému řízení s jednotnou zápornou zpětnou vazbou v uzavřené smyčce spolu s proporcionálně integrálním regulátorem je znázorněno na následujícím obrázku.
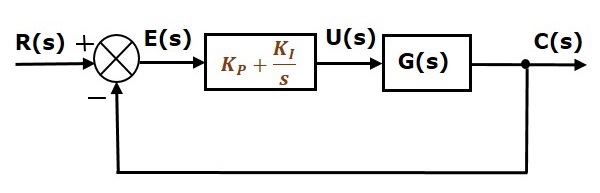
Proporcionálně integrální regulátor se používá ke snížení chyby ustáleného stavu bez vlivu na stabilitu řídicího systému.
Proporcionálně integrální derivační regulátor (PID)
Proporcionálně integrální derivační regulátor vytváří výstup, který je kombinací výstupů proporcionálního, integrálního a derivačního regulátoru.
$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}$$
Použijeme Laplaceovu transformaci na obě strany -.
$$U(s)=\levá(K_P+\frac{K_I}{s}+K_D s \pravá )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$
Takže, přenosová funkce proporcionálního integrálního derivačního regulátoru je $K_P + \frac{K_I} {s} + K_D s$.
Blokové schéma uzavřeného řídicího systému s jednotnou zápornou zpětnou vazbou spolu s proporcionálně integrálním derivačním regulátorem je znázorněno na následujícím obrázku.
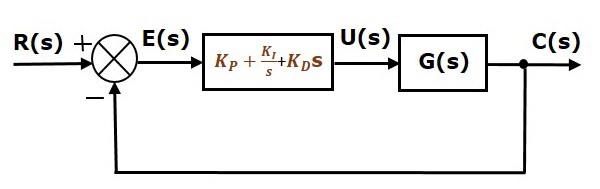
Proporcionálně integrální derivační regulátor se používá ke zlepšení stability řídicího systému a ke snížení chyby ustáleného stavu.
.