Die verschiedenen Arten von Controllern werden verwendet, um die Leistung von Kontrollsystemen zu verbessern. In diesem Kapitel werden wir die grundlegenden Regler wie den Proportional-, den Derivativ- und den Integralregler besprechen.
Proportionalregler
Der Proportionalregler erzeugt einen Ausgang, der proportional zum Fehlersignal ist.
$$u(t) \propto e(t) $$
$$$\Rechtspfeil u(t)=K_P e(t)$$
Anwenden der Laplace-Transformation auf beide Seiten –
$$U(s)=K_P E(s)$$
$$$\frac{U(s)}{E(s)}=K_P$$
Daher, ist die Übertragungsfunktion des Proportionalreglers $K_P$.
Wobei,
U(s) die Laplace-Transformierte des Stellsignals u(t)
E(s) die Laplace-Transformierte des Fehlersignals e(t)
KP die Proportionalitätskonstante ist
Das Blockschaltbild der Einheitsgegenkopplungs-Regelstrecke mit dem Proportionalregler ist in der folgenden Abbildung dargestellt.
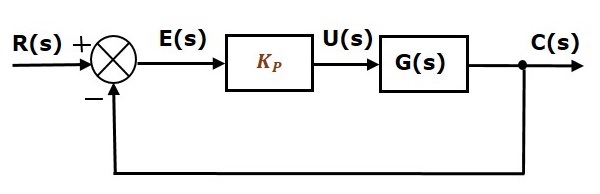
Der Proportionalregler wird verwendet, um das Einschwingverhalten je nach Anforderung zu verändern.
Derivationsregler
Der Derivationsregler erzeugt einen Ausgang, der vom Fehlersignal abgeleitet ist.
$$u(t)=K_D \frac{\text{d}e(t)}{\text{d}t}$$
Wenden Sie die Laplace-Transformation auf beide Seiten an.
$$U(s)=K_D sE(s)$$
$$$\frac{U(s)}{E(s)}=K_D s$$
Daher ist die Übertragungsfunktion des Ableitungsreglers $K_D s$.
Wobei $K_D$ die Ableitungskonstante ist.
Das Blockschaltbild der Einheitsgegenkopplungs-Regelstrecke mit dem Ableitungsregler ist in der folgenden Abbildung dargestellt.
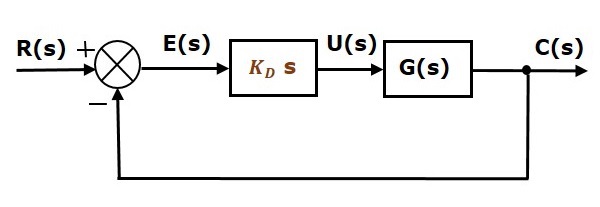
Der Ableitungsregler wird verwendet, um aus der instabilen Regelstrecke eine stabile zu machen.
Integralregler
Der Integralregler erzeugt einen Ausgang, der ein Integral des Fehlersignals ist.
$$u(t)=K_I \int e(t) dt$$
Anwenden der Laplace-Transformation auf beide Seiten –
$$U(s)=\frac{K_I E(s)}{s}$$
$$$frac{U(s)}{E(s)}=\frac{K_I}{s}$$
Daher, ist die Übertragungsfunktion des Integralreglers $\frac{K_I}{s}$.
Wobei $K_I$ die Integralkonstante ist.
Das Blockschaltbild der Einheitsgegenkopplungs-Regelstrecke mit dem Integralregler ist in der folgenden Abbildung dargestellt.
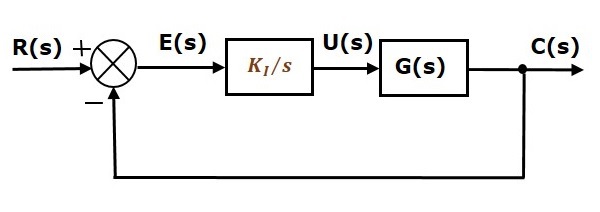
Der Integralregler wird zur Verringerung der stationären Regelabweichung eingesetzt.
Lassen Sie uns nun die Kombination der Grundregler besprechen.
Proportional-Derivativ (PD)-Regler
Der Proportional-Derivativ-Regler erzeugt einen Ausgang, der die Kombination der Ausgänge von Proportional- und Derivativ-Regler ist.
$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}$$
Wenden Sie die Laplace-Transformation auf beide Seiten an.
$$U(s)=(K_P+K_D s)E(s)$$
$$$\frac{U(s)}{E(s)}=K_P+K_D s$$
Daher, ist die Übertragungsfunktion des proportionalen Ableitungsreglers $K_P + K_D s$.
Das Blockschaltbild der Einheitsgegenkopplungs-Regelstrecke mit dem Proportional-Differenzialregler ist in der folgenden Abbildung dargestellt.
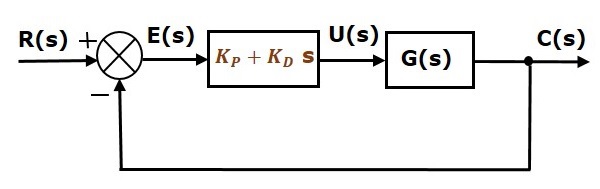
Der Proportional-Derivativ-Regler wird verwendet, um die Stabilität der Regelstrecke zu verbessern, ohne die stationäre Regelabweichung zu beeinflussen.
Proportional-Integral (PI)-Regler
Der Proportional-Integral-Regler erzeugt einen Ausgang, der die Kombination der Ausgänge des Proportional- und des Integral-Reglers ist.
$$u(t)=K_P e(t)+K_I e(t) dt$$
Wenden Sie die Laplace-Transformation auf beide Seiten an –
$$U(s)=\left(K_P+\frac{K_I}{s} \right )E(s)$$
$$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$
Daher, ist die Übertragungsfunktion des Proportional-Integral-Reglers $K_P + \frac{K_I} {s}$.
Das Blockschaltbild der Einheitsgegenkopplungsregelung mit dem Proportional-Integral-Regler ist in der folgenden Abbildung dargestellt.
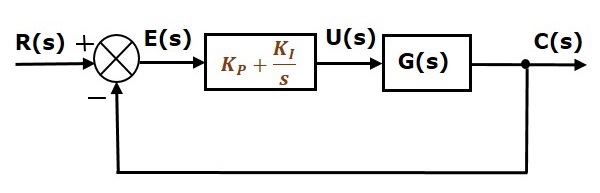
Der Proportional-Integral-Regler dient zur Verringerung der stationären Regelabweichung, ohne die Stabilität der Regelstrecke zu beeinträchtigen.
Proportional-Integral-Derivativ-Regler (PID-Regler)
Der Proportional-Integral-Derivativ-Regler erzeugt einen Ausgang, der die Kombination der Ausgänge von Proportional-, Integral- und Derivativ-Regler ist.
$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}$$
Wenden Sie die Laplace-Transformation auf beide Seiten an.
$$U(s)=\left(K_P+\frac{K_I}{s}+K_D s \right )E(s)$$
$$$frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$
Daher, ist die Übertragungsfunktion des Proportional-Integral-Differential-Reglers $K_P + \frac{K_I} {s} + K_D s$.
Das Blockschaltbild der Einheitsgegenkopplungsregelung mit dem Proportional-Integral-Differenzial-Regler ist in der folgenden Abbildung dargestellt.
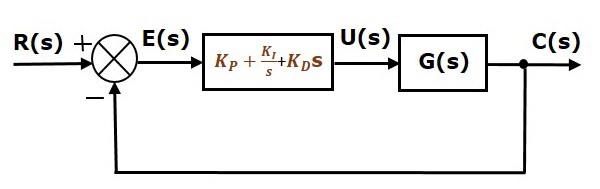
Der Proportional-Integral-Differenzial-Regler wird verwendet, um die Stabilität der Regelung zu verbessern und den stationären Fehler zu verringern.