GENERAL CHEMISTRY TOPICS
Energie: Grundlegende Konzepte
Formen der Energie: Kinetisch und potentiell.Arbeit und Energie.Wärme und Temperatur.Elektrostatische potentielle Energie.
Energie: kinetisch und potentiell
Das Konzept der Energie ist grundlegend für die physikalischen Wissenschaften. Wir wollen hier einige erste Grundsätze zur Energie darlegen und einige Formen der Energie vorstellen, die für die Chemie von besonderer Bedeutung sind. Zunächst einmal ist es oft sehr nützlich, ein System als einen bestimmten Teil des Universums zu definieren, an dem unsere Beobachtungen gemacht werden. Das System besteht aus einem Objekt oder einer Ansammlung von Objekten und wird vom Rest des Universums – den wir als Umgebung bezeichnen – durch eine reale oder imaginäre Grenze abgegrenzt.
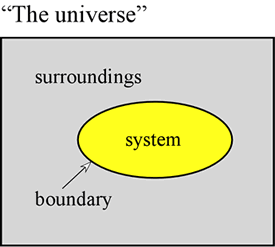
Eine Gasprobe innerhalb eines festen Volumens, z. B. eines Metallzylinders, ist ein Beispiel für ein System – eines, das für uns von Bedeutung sein wird, wenn wir uns mit den allgemeinen Eigenschaften von Gasen befassen. Weitere Beispiele sind eine Gasprobe in einem Ballon oder ein Verbrennungsgemisch in einem Zylinder mit einem Kolben. In beiden Fällen ist das System von einer physikalischen, aber beweglichen Grenze umgeben, so dass das Volumen des Systems nicht festgelegt ist. Ein weiteres Beispiel, das wir häufig betrachten werden, ist ein Stoffgemisch in Lösung, das in einem Reagenzglas oder Becherglas eine chemische Reaktion durchläuft. Die hier eingeführte Terminologie ist von besonderer Bedeutung für die Untersuchung der Energie in chemischen Systemen, die größtenteils in den Bereich der Thermodynamik fällt.
In der allgemeinen Chemie befinden sich die von uns betrachteten Systeme in der Regel in Ruhe und Gravitationseffekte werden ignoriert. Oft sind wir an Systemen interessiert, in denen chemische Reaktionen ablaufen, wobei sich die chemische Zusammensetzung des Systems mit der Zeit ändert. Lassen Sie uns jedoch eine breitere Perspektive einnehmen, indem wir mechanische Systeme wie ein schwingendes Pendel oder rollende und kollidierende Billardkugeln heranziehen, um die allgemeinen Prinzipien der Energie zu verstehen.
Ein System kann auf zwei verschiedene Arten Energie besitzen, die wir kinetische und potentielle Energie nennen. Kinetische Energie ist die Energie der Materie in Bewegung. In der Physik gibt es eine genaue mathematische Definition der kinetischen Energie (KE), die in der Gleichung (unten links) dargestellt ist.
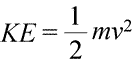
Die kinetische Energie eines Objekts wird hier als Produkt aus der Masse des Objekts (m) und dem Quadrat seiner Geschwindigkeit (v), ebenfalls multipliziert mit der Konstante ½, dargestellt. Besteht das System aus mehreren Objekten, kann die gesamte kinetische Energie als Summe der kinetischen Energien der einzelnen Objekte ausgedrückt werden.
Aus dieser Definition lassen sich Einheiten für die Energie ableiten. Die SI-Einheit für Energie ist das Joule (J), das wie folgt definiert ist:
1 J = 1 kg-m-s-2
Potentielle Energie ist die Energie eines Systems, die typischerweise in irgendeiner Form in kinetische Energie umgewandelt werden kann und in der Lage ist, in gewissem Maße eine als Arbeit bezeichnete Größe zu erzeugen (wird weiter unten erläutert). Ein anschauliches Beispiel für potenzielle Energie ist ein Ziegelstein auf dem Sims eines Gebäudes. Der Ziegelstein besitzt aufgrund seiner Höhe, d. h. seines Standorts in Bezug auf ein Gravitationsfeld, eine bestimmte Menge potenzieller Energie. Wenn wir dem Ziegelstein einen Schubs geben, so dass er von der Kante fällt, bewegt er sich spontan in die Richtung der niedrigeren potenziellen Gravitationsenergie und gewinnt dabei kinetische Energie. Ein weiteres Beispiel ist die elektrische potenzielle Energie einer Batterie (die in Form von Spannung ausgedrückt wird). Wenn man einen Stromkreis mit einem Draht und einer Glühbirne herstellt, der die beiden Pole einer Batterie verbindet, bewirkt der Unterschied im elektrischen Potential zwischen ihnen, dass sich die Elektronen im Draht bewegen (kinetische Energie), was zur Erzeugung von Wärme und Licht führt.
Ein wichtiger allgemeiner Grundsatz über Energie ist, dass sie weder erzeugt noch zerstört werden kann. Dies ist bekannt als das Gesetz der Energieerhaltung. Quantitativ bedeutet dies, dass in einem System wie dem fallenden Ziegelstein oder dem Pendel einer Uhr die Summe aus kinetischer und potentieller Energie konstant ist. Dies ist eine gewisse Abstraktion, denn bei einem realen Pendel geht ständig ein Teil der Energie durch Reibung verloren, und dem Pendel muss eine kleine Menge Energie zugeführt werden, damit es weiterschwingt (und die Uhr funktioniert). Berücksichtigt man jedoch diese „verlorene“ Energie (die sich in Wirklichkeit als Anstieg der Wärmeenergie der umgebenden Luftmoleküle zeigt) durch sorgfältige experimentelle Messungen, so stellt man fest, dass die Energie tatsächlich immer erhalten bleibt. Ein weiterer Vorbehalt ist in Einsteins berühmter Gleichung E = mc2 zusammengefasst, die eine grundlegende Äquivalenz von Masse und Energie ausdrückt. Eine allgemeinere Form des Energieerhaltungssatzes, der als Masse-Energie-Erhaltungssatz bezeichnet werden kann, trägt dieser Gleichwertigkeit Rechnung. Um auf die allgemeine Chemie zurückzukommen: Solche Materie-Energie-Umwandlungen sind nicht typisch für sie, während die Untersuchung von Kernreaktionen und Radioaktivität in den Bereich der Kernphysik fällt.
Betrachten wir eine chemische Reaktion, bei der chemische Veränderungen mit der Erzeugung von Wärme einhergehen, so stellt sich eine Frage: Wie steht es in diesem Fall mit der Erhaltung der Energie? Die Antwort ist, dass es eine Form von potenzieller Energie gibt, die wir als chemische potenzielle Energie (oder einfach chemisches Potenzial) bezeichnen können, die in der molekularen Zusammensetzung der Reaktanten steckt. Diese potenzielle Energie wird dann in Energie in Form von Wärme umgewandelt, aber es stellt sich heraus, dass die Nettomenge der vorhandenen Energie konstant bleibt, sobald wir in der Lage sind, die Wärmeerzeugung zu definieren und zu messen. Ein alltägliches Beispiel für das, was wir heute als chemische potenzielle Energie verstehen, ist ein Benzinmotor, in dem das Gemisch aus Benzin und Sauerstoff eine latente Form von Energie besitzt. Diese latente Energie im Benzin-Sauerstoff-Gemisch wird verbraucht, um die kinetische Energie eines Autos zu erzeugen.
Arbeit und Energie
Arbeit ist ein weiterer Begriff, der in der Physik eine genaue Definition zulässt. Darüber hinaus können die Gesetze der Mechanik mit Hilfe des Arbeit-Energie-Theorems mit der Energie verknüpft werden. Der Abstoß eines Fußballs oder eine beliebige Anzahl ähnlicher Beispiele veranschaulicht die Idee, dass die kinetische Energie eines Objekts durch Anwendung einer Kraft erhöht werden kann. Das Arbeit-Energie-Theorem, das eine Verallgemeinerung dieses Gedankens darstellt, lässt sich grob wie folgt formulieren: Die Änderung der Energie, die ein Gegenstand besitzt, ist gleich der Größe der auf ihn wirkenden Kraft, multipliziert mit der Strecke, durch die die Kraft wirkt.
Die Energieänderung, die in einem System als Folge von Arbeit auftritt, kann aus der Sicht des Systems positiv oder negativ sein. Arbeit kann von einem System geleistet werden, oder ein System kann von der Umgebung mit Arbeit belastet werden. Wird von einem System Arbeit verrichtet, verliert es Energie an die Umgebung. Wenn das System Arbeit verrichtet, wird die Energie des Systems erhöht. Wenn beispielsweise ein Funke, der ein Verbrennungsgemisch in einem Zylinder mit einem beweglichen Kolben in Gang setzt, eine schnelle Ausdehnung des Systems bewirkt und die Ausdehnung mechanisch mit der Bewegung einer Stange in der Umgebung gekoppelt ist, verrichtet das System des Zylinders Arbeit an der Umgebung und verliert dabei Energie. Dies ist natürlich ein Teil davon, wie ein Verbrennungsmotor chemische potentielle Energie in die kinetische Energie eines sich bewegenden Autos umwandelt.
Eine Folge des Arbeit-Energie-Satzes betrifft die Einheiten, nämlich dass die Arbeit in denselben Einheiten gemessen werden kann wie die Energie. Da das zweite Newtonsche Gesetz Kraft = Masse × Beschleunigung lautet, wird das Newton (N), die SI-Einheit für Kraft, abgeleitet als M × L × T -2, und somit ist 1 N = 1 kg m s-2. Kraft mal Weg hat die Größen M × L2 × T -2, und somit ist die SI-Einheit für Energie, das Joule (J), definiert als 1 J = 1 kg m2 s-2. An dieser Stelle solltest du selbst überprüfen, dass die Gleichung für die kinetische Energie dieselbe Kombination aus den Grundgrößen Masse (M), Länge (oder Abstand, L) und Zeit (T) beinhaltet.
Wärme und Temperatur
Wir verwenden die Begriffe Wärme und Temperatur recht häufig und sprechen oft von Wärme als einer Form von Energie. Wir haben alle ein intuitives Gefühl dafür, was diese Dinge sind, aber hier wollen wir sie wissenschaftlicher betrachten und ihnen, wenn möglich, formale Definitionen geben. Dies ist eine notwendige Voraussetzung für die Quantifizierung der Energie, die der Wärme entspricht, und damit für Messungen, mit denen der Energieerhaltungssatz überprüft werden kann. Wir stellen fest, dass die Wärmeenergie eines Systems mit der gesamten kinetischen Energie (wie oben definiert) der Atome und Moleküle, aus denen es besteht, gleichgesetzt werden kann. Die Temperatur eines Objekts oder Systems ist tatsächlich ein Maß für die durchschnittliche kinetische Energie der Atome und/oder Moleküle, aus denen es besteht. (Anmerkung: Die Temperatur ist nicht genau gleich der durchschnittlichen kinetischen Energie der Moleküle, aber sie ist direkt proportional dazu. Weitere Einzelheiten finden Sie auf der Webseite zur kinetischen Molekulartheorie).
Eine Möglichkeit zur Veranschaulichung dessen, was wir mit Wärme und Temperatur meinen, und der Unterscheidung zwischen ihnen, ist die Analogie zu einer Billardkugel. In einigen einfachen Zusammenhängen ist das Verhalten von Billardkugeln ein adäquates Modell für eine Ansammlung von Atomen oder Molekülen, z. B. in einer Gasprobe. Genau wie Billardkugeln, die gerade von einer sich schnell bewegenden Spielkugel getroffen wurden, bewegen sich die Moleküle eines Gases hin und her, prallen aneinander und an den Wänden des Behälters ab, in dem sie sich befinden. Die kinetische Gesamtenergie der Billardkugeln, die sich aus der Summe der kinetischen Energie der einzelnen Kugeln ergibt, entspricht dem thermischen Energiegehalt einer Gasmolekülprobe. Bei einem „Break“ zu Beginn eines Billardspiels verteilt sich die anfängliche kinetische Energie der Spielkugel auf alle Kugeln auf dem Tisch. Einige bewegen sich recht schnell, andere nicht so schnell, aber die Analogie zur „Wärme“ oder „thermischen Energie“ für das System der Billardkugeln ist einfach die Summe dieser kinetischen Energien. Andererseits wäre die Temperatur des Billardkugelsystems proportional zur durchschnittlichen kinetischen Energie des Kugelensembles.
Elektrostatische potentielle Energie
Das Gesetz der elektrostatischen Anziehung und Abstoßung oder Coulomb-Gesetz beschreibt die Kraft, die auf ein geladenes Objekt durch die Anwesenheit eines anderen geladenen Objekts ausgeübt wird. Die Kraft ist am einfachsten zu berechnen, wenn die Ladungen als sehr kleine Punktladungen behandelt werden können. Die Größe der Kraft, die ein geladenes Objekt „spürt“, ist proportional zum Produkt der Ladungen (die SI-Einheit für elektrische Ladung ist Coulomb, C) und umgekehrt proportional zum Quadrat des Abstands zwischen den Ladungen (r in der Abbildung rechts). Die Kraft ist eine anziehende Kraft (wie die Schwerkraft und in der Abbildung durch nach innen gerichtete Pfeilspitzen gekennzeichnet), wenn die Ladungen entgegengesetzte Vorzeichen haben, und eine abstoßende Kraft, wenn die Ladungen das gleiche Vorzeichen haben.
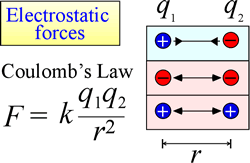
Wenn Kräfte (wie elektrostatische, magnetische und Gravitationskräfte) in einer Entfernung (durch den Raum, ohne mechanischen Kontakt) wirken können, sagt man, dass sich die Objekte, die solchen Kräften ausgesetzt sind, in einem potenziellen Energiefeld befinden. Wir haben bereits über die potenzielle Gravitationsenergie gesprochen, und ähnlich verhält es sich bei den elektrostatischen Kräften: Ein geladenes Objekt hat elektrostatische potenzielle Energie, weil es sich in einem elektrischen Feld befindet. Ein solches Feld existiert in der Nähe jeder anderen Ladung oder Ladungen.
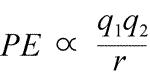
Gleichung für elektrostatische potentielle Energie: PE ist proportional zu den Ladungen q1 und q2 und umgekehrt proportional zum Abstand r. Die Form der potentiellen Energiefunktion folgt mathematisch aus dem Kraftausdruck, dem Coulomb-Gesetz.
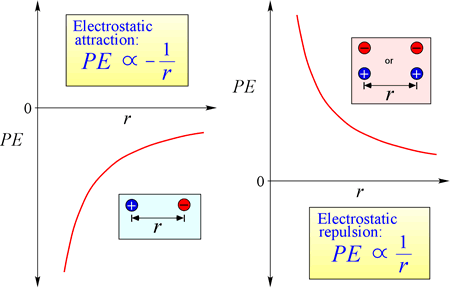
Da die Ladungen bei der Anziehung entgegengesetzte Vorzeichen haben, ist die potentielle Energie immer negativ, und je mehr sich die Ladungen annähern, desto negativer – d.h. desto geringer – wird die potentielle Energie. Wenn der Abstand r gegen Null geht, wird die potenzielle Energie unendlich negativ. Für Ladungen mit gleichem Vorzeichen ist die Abstoßungsenergie immer positiv und wird unendlich positiv, wenn der Abstand r gegen Null geht.
Die elektrostatische potentielle Energie ist ein wichtiger Faktor in der Chemie. Das Verständnis der Natur des Atoms, der chemischen Bindung und der zwischenmolekularen Kräfte ist absolut abhängig von der Berücksichtigung des Einflusses von Ladungs-Ladungs-Wechselwirkungen, die zur Energie eines Systems beitragen.
Wichtige Einheiten
Energie (SI-Einheit) 1 Joule = 1 J = 1 kg-m-s-2
Elementarladung, e = 1,60218 × 10-19 C (Coulomb, C)
Faraday-Konstante: F = NAe = 9,64853 × 104 C-mol-1
Elektrisches Potential: Volt, V 1 V = 1 J C-1