Du bist ein verzweifelter Student, der versucht, seine letzte Hausarbeit vor dem Abschluss zu schreiben. Du willst nur noch fertig werden und deine Leistung feiern. Plötzlich kommt jemand in die Kabine, in der Sie den ganzen Tag gearbeitet haben. Diese Person sieht Ihnen sehr ähnlich, aber Sie haben keine Zeit herauszufinden, was los ist, denn sie gibt Ihnen sofort einen USB-Stick und sagt Ihnen, dass Sie die Hausarbeit, die sich auf dem Stick befindet, abgeben sollen. „Dann können Sie feiern gehen“, sagt sie lächelnd, während sie schnell das nahe gelegene Treppenhaus betritt. Du stehst auf und gehst ihr nach, aber sie scheint verschwunden zu sein.
Du gehst zurück zu deinem Arbeitsplatz, öffnest die Datei der Hausarbeit, liest sie schnell durch und gibst die Arbeit ab, wobei du dein ethisches Dilemma verdrängst. Ein paar Tage später erhalten Sie Ihre Note: eine Eins plus. Sie machen sich auf die Suche nach dem mysteriösen Fremden, der Ihnen diese wunderbare Arbeit gegeben hat, und landen wieder im Treppenhaus. Du gehst hinein und überlegst, wo der Fremde wohl hingegangen sein könnte. Nach ein oder zwei Augenblicken gehst du. Als du an der Kabine vorbeikommst, in der du so lange geschuftet hast, siehst du dich selbst! Dann dämmert es Ihnen. Sie müssen sich selbst das Papier geben. Zum Glück hatten Sie den USB-Stick in Ihre Tasche gesteckt, und da Sie ein äußerst ungepflegter Student sind, haben Sie immer noch die gleiche Hose an. Du gehst in die Kabine, übergibst dir den USB-Stick, gibst dir ein paar Anweisungen und flüchtest zurück ins Treppenhaus, das dich in deine Gegenwart zurückbringt.
Wie kannst du dir eine Arbeit geben, die niemand geschrieben hat? Wie kann die Abgabe der Arbeit dazu führen, dass Sie die Arbeit abgeben?
Was sind Kausalschleifen?
Eine Kausalschleife ist eine Folge von Ereignissen e1, … , en. Jedes Ereignis in der Schleife ist eine der Ursachen für das nächste Ereignis. Das letzte Ereignis en ist eine der Ursachen für das erste Ereignis e1. Wenn eine Kausalschleife keine externen (außerhalb der Schleife liegenden) Ursachen oder Wirkungen hat, dann ist diese Kausalschleife eine geschlossene Kausalschleife; andernfalls ist sie eine offene Kausalschleife. Stellen Sie sich geschlossene Kausalschleifen als kausal isoliert vor. Offene Kausalschleifen sind kausal eingebettet.
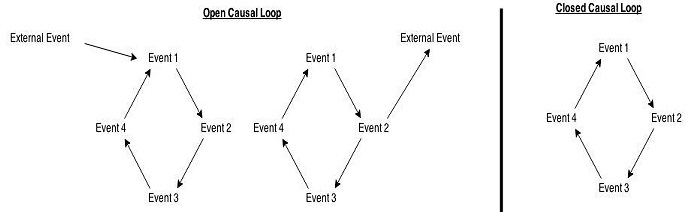
Abbildung 1: Zwei Arten von Kausalschleifen
Sind Kausalschleifen unmöglich?
Die Idee von Kausalschleifen wird manchmal als ein inhärentes Paradoxon angesehen. Die Gründe für diese Besorgnis sind unterschiedlich.
Grund 1: Für jedes Ereignis muss es eine erste Ursache ohne Ursache geben. Schleifen können ex nihilo (aus dem Nichts) erscheinen, scheinbar ohne eine letzte erste Ursache. Diese Bedenken lassen sich ausräumen, wenn man Kausalschleifen mit gewöhnlichen Kausalketten vergleicht. Eine Kausalkette ist eine Abfolge von Ereignissen, wobei jedes Ereignis das nächste Ereignis in der Abfolge verursacht (eine Kausalschleife ist eine besondere Art von Kausalkette). Einige Kausalketten bilden keine Schleife; sie bestehen aus Ereignissen in einer Abfolge, wobei jedes Ereignis zeitlich auf das nächste Ereignis in der Abfolge folgt und dieses verursacht. In dieser Definition steht nichts davon, dass die Kette einen Anfang (oder ein Ende) haben muss. Daher erscheint es etwas seltsam, darauf zu bestehen, dass Ereignisse in einer Kausalschleife eine letzte erste Ursache benötigen. Der einzige Unterschied zwischen Kausalketten und Kausalschleifen besteht darin, dass man, wenn man der Kausalität entlang einer Kausalschleife folgt, am Ende wieder dort landet, wo man angefangen hat.
Darüber hinaus haben Kausalschleifen eine erste Ursache und scheinen sogar dazu verpflichtet zu sein, eine erste Ursache zu haben. In jeder Kausalschleife gibt es mindestens ein Ereignis, das früher eintritt als alle anderen. Dieses Ereignis muss sich nicht immer als eine ultimative erste Ursache erweisen, die die gesamte Schleife erklärt. Da das Anfangsereignis jedoch vor den anderen Ereignissen in der Zeitachse eintritt, ist es das erste. Es ist das früheste Ereignis in der Schleife.
Grund 2: Die Gefahr einer zirkulären Erklärung. Betrachten wir „früher-als“, eine Beziehung, die oft mit einem Ereignis in Verbindung gebracht wird, das ein anderes Ereignis verursacht. Traditionell wird diese Beziehung als transitiv angesehen, d. h. wenn Ereignis a früher als Ereignis b und Ereignis b früher als Ereignis c ist, dann ist Ereignis a früher als Ereignis c. Wenn man jedoch davon ausgeht, dass Kausalität transitiv ist, und sie auf eine Kausalschleife anwendet, bricht die Sache zusammen. Wenn Kausalität transitiv ist, dann ist jedes Ereignis in einer Kausalschleife eine Ursache für sich selbst. In einer Kausalschleife mit drei Ereignissen funktioniert die Kausalität hervorragend, um zu sagen, dass Ereignis a Ursache für b ist und b Ursache für c ist und c Ursache für a ist, aber wenn die Kausalität nicht transitiv ist, führen diese drei Tatsachen zu der Schlussfolgerung, dass a Ursache für a ist. Dass a Ursache für a ist, ist sicherlich keine informative Erklärung für a. Glücklicherweise müssen wir, selbst wenn die Kausalität transitiv ist, nicht annehmen, dass die entsprechenden erklärenden Verbindungen erhalten bleiben. Ulrich Meyer (2012, 261) behauptet, dass die Kombination aller lokalen Erklärungen zu einer schwächeren Erklärung führt.
Grund 3: Für jede Ereignisfolge muss es eine hinreichende Erklärung geben, warum die Folge so auftritt, wie sie auftritt. Wenn es für jede Ereignisfolge eine hinreichende Erklärung geben muss, wird das mögliche Problem durch die Betrachtung von Dschinns erhellt. Ein Dschinn ist ein Objekt, das Teil der Ereignisse in der Schleife ist und aus dem Nichts zu entstehen scheint. Ein hervorragendes Beispiel für einen Dschinn ist Swanns Halskette aus Timerider: The Adventure of Lyle Swann.
In diesem Film aus dem Jahr 1982 wird Swann versehentlich in der Zeit zurückgeschickt und trifft eine Frau namens Claire, die ihn schließlich verführt. Nach einer Reihe von spektakulären Ereignissen wird Swann von den Leuten, die ihn versehentlich in die Vergangenheit befördert haben, gerettet. Kurz bevor er gerettet wird, schnappt sich Claire die Halskette, die Swann von seiner Ur-Ur-Großmutter erhalten hat, die sie seinem Ur-Ur-Großvater gestohlen hatte. Die Halskette ist ein Dschinn, denn Swann erhält sie von seiner Ururgroßmutter, die ihm dieselbe Halskette Jahre zuvor gestohlen hat. Wie Sie vielleicht schon erraten haben, ist Claire Swanns Ur-Ur-Großmutter. Swann selbst ist sein eigener Ururgroßvater.
Das Problem, das sich bei der Halskette und den meisten Dschinns stellt, ist die Quelle ihrer Existenz. Wie kann ein physischer Gegenstand wie eine Halskette einfach so existieren? Wer hat die Halskette entworfen? Was erklärt, warum es eine Halskette ist und nicht etwa ein Armband? Es muss eine Erklärung dafür geben, warum die Halskette so ist, wie sie ist. Richtig?
Es gibt Erklärungen für die Phasen der Existenz der Halskette. Die Halskette hat Ursachen. Dass Swann die Halskette von seiner Großmutter erhalten hat, ist eine Ursache dafür, dass er sie mit in die Vergangenheit genommen hat. Dass die Halskette in der Zeit zurückgeht, ist eine Ursache dafür, dass Claire die Halskette stehlen kann, und so weiter. Darüber hinaus könnte man argumentieren, dass das Universum und die Naturgesetze eine bestimmte Struktur haben müssen, damit Kausalschleifen existieren können. Diese Gesetze wären auch eine Quelle für nützliche Erklärungen.

Abbildung 2: Timerider Timeline
Einige Tatsachen scheinen jedoch zwangsläufig unerklärt zu bleiben, Tatsachen wie die, dass die Halskette eine Halskette ist und nicht ein Armband. Und warum gibt es eine Kausalschleife und keine Kausalschleife? Zeigt unsere Unfähigkeit, diese Fakten zu erklären, dass Kausalschleifen etwas Inkohärentes an sich haben? Nein; das Problem bei dieser Argumentation ist, dass sich ähnliche Fragen bei normalen Objekten stellen. Man kann die Ursachen eines Stuhls erkennen, weil man sehen kann, wie der Tischler den Stuhl aus Holz gebaut hat, aber wie ist das Holz entstanden? Mehr noch, wie sind die Atome entstanden, aus denen das Holz besteht? Man kann diese Fragen immer wieder stellen, aber eine völlig ausreichende und vollständige Erklärung ist unter normalen Umständen so gut wie unmöglich zu finden. Es gibt viele Tatsachen und Gegenstände, für die wir vielleicht nie eine gute Erklärung finden werden.
Um diese Analyse einen Schritt weiter zu führen, betrachten wir den Ursprung der künstlerischen Gestaltung der Halskette. Die Halskette schien eine normale Halskette zu sein, die mit Absicht und Kunstfertigkeit angefertigt worden war. Das wirft die Frage auf, woher die Kunstfertigkeit stammt. Wessen (oder wessen) Fähigkeiten und Kenntnisse flossen in die Herstellung dieser Halskette ein? Storrs McCall (2010) sagt, dass es keine Lösung für dieses Problem gibt. Vielleicht gibt es für manche Fakten einfach keine Erklärung. Darauf zu bestehen, dass alles eine Erklärung haben muss, ist nicht gerechtfertigt.
Erfordern Zeitreisen kausale Schleifen?
Die Behauptung, dass alle Zeitreisen mindestens eine kausale Schleife enthalten müssen, ist weit verbreitet. In seinem 2009 erschienenen Aufsatz zu diesem Thema stellt Bradley Monton diese Position anhand eines Zitats von D.H. Mellor dar. Monton zufolge argumentiert Mellor gegen die Möglichkeit von Zeitreisen, indem er „die kausalen Schleifen ausschließt, die zyklische Zeit und rückwärts gerichtete Zeitreisen benötigen“ (Monton, 2009, 55; Mellor 1998, 131). Wenn ein Zeitreisender in die Vergangenheit reist, werden seine Handlungen in der Vergangenheit immer Auswirkungen haben, die die Reise des Zeitreisenden in die Vergangenheit beeinflussen.
Hier ist ein einfaches Beispiel für dieses Phänomen: Im Jahr 2020 baut Jim eine Zeitmaschine aus einigen Plänen, die er auf seinem Dachboden gefunden hat, und beschließt, zurückzureisen, um sein jüngeres Ich zu sehen. Jim reist also zurück ins Jahr 1990 und findet sein jüngeres Ich. Jim gibt seinem jüngeren Ich die Pläne für die Zeitmaschine. Sein jüngeres Ich findet die Idee von Zeitreisen absurd und verstaut die Pläne auf seinem Dachboden. Im Jahr 2020 findet Jim diese Pläne und baut seine Zeitmaschine.
Dass Jim sein Zeitreiseabenteuer antreten kann, hängt eindeutig davon ab, dass er sich überhaupt auf das Abenteuer einlässt. Jims Handlungen oder auch nur seine bloße Anwesenheit bei der Ankunft könnten sein jüngeres Ich in einer Weise beeinflusst haben, die zu seiner Reise in die Vergangenheit führt. Mehr noch, es scheint, dass jede Reise in die Vergangenheit in irgendeiner Weise mit Menschen, Objekten oder Partikeln interagiert, die sich schließlich von der Vergangenheit in die Zukunft bewegen, was bedeutet, dass jede Zeitreise zu einer Kausalschleife führt. Das Potenzial für eine Veränderung, die auf irgendeine Weise eine Kette von Ereignissen auslöst, die die Reise in die Vergangenheit, die die ursprüngliche Veränderung hervorgebracht hat, beeinflusst, scheint echt zu sein.
Doch nur das Potenzial zu haben, ein Ereignis zu verursachen, bedeutet nicht, dass das Ereignis auch eintritt. Monton behauptet, eine hypothetische Situation gefunden zu haben, die Zeitreisen ohne kausale Schleifen beinhaltet. Er beschreibt ein Universum, das in zwei Regionen aufgeteilt ist, die nur A-, B- und C-Teilchen enthalten. (Siehe Abbildung 1.) Region 1 enthält nur A- und C-Teilchen und den Bereich bis zur Grenze der beiden Regionen. Region 2 enthält nur B- und C-Teilchen und das Gebiet bis einschließlich der gleichen Grenze. Ein Kraftfeld hindert die B-Teilchen daran, die Grenze zur Region 1 zu überschreiten. Die C-Teilchen interagieren weder mit A- noch mit B-Teilchen und bewegen sich frei zwischen den Regionen 1 und 2. Wenn ein A-Teilchen die Grenze überschreitet, wird es sofort in ein B-Teilchen umgewandelt.
Betrachten Sie nun das folgende Szenario: Ein A-Teilchen bewegt sich auf die Grenze zu. Im selben Moment, in dem das Teilchen die Grenze erreicht, wird es in ein B-Teilchen umgewandelt und beginnt ebenfalls, in der Zeit zurückzureisen. Während der Zeitreise folgt das A-Teilchen der Grenze, so dass das A-Teilchen mit keinem der anderen Teilchen in Wechselwirkung treten kann. Ausgehend von den Anfangsbedingungen dieses Beispiels ist dieses A-Teilchen das einzige, das die Grenze erreichen kann. Sobald das Teilchen seine Zeitreise beendet, bewegt sich das A-Teilchen in die Region 2 (Monton 2009, 60).
Abbildung 3: Montons Beispiel
Es scheint, dass das A-Teilchen in der Lage ist, Zeitreisen zu unternehmen, ohne mit irgendeinem der Teilchen in einer der beiden Regionen zu interagieren, einschließlich seines jüngeren Selbst. Während der Zeitreise in die Vergangenheit und nachdem es die Zeitreise beendet hat, verhindert die Grenze, dass das Teilchen mit seiner Abreise in die Vergangenheit in Wechselwirkung tritt. Das bedeutet, dass Teilchen A erfolgreich durch die Zeit gereist ist, ohne in eine Kausalschleife einzutreten, da die Zeitreise des Teilchens A nicht dazu geführt haben kann, dass eben dieses Teilchen seine Zeitreise begonnen hat.
Im Allgemeinen, insbesondere in realistischeren Situationen, in Situationen mit einer Physik, die unserer eigenen ähnlicher ist, scheint das Konzept der Zeitreise in die Vergangenheit ohne das Auftreten von Kausalschleifen in irgendeiner Form unwahrscheinlich. Es bedarf einer äußerst sorgfältigen und spezifischen Beschreibung, um das clevere Szenario von Monton zu erzeugen.
Do Causal Loops Require Time Travel?
Eine Kausalschleife wird immer eine Rückwärtsverursachung enthalten, einfach weil irgendwann eines der Ereignisse in der Schleife die Ursache eines früheren Ereignisses sein muss. Das beweist jedoch nicht, dass alle Kausalschleifen Zeitreisen beinhalten. Beinhaltet die Rückwärtsverursachung immer Zeitreisen?
Manchmal nein, manchmal ja. In einem Universum, in dem Objekte nur auf ein Objekt einwirken können, das zur gleichen Zeit wie sie selbst existiert, wären Zeitreisen notwendig, um Objekte zu einem früheren Zeitpunkt zu beeinflussen. Damit ein Objekt Objekte in einer anderen Zeit als seiner eigenen Zeit beeinflussen kann, müsste das Objekt in die andere Zeit reisen und zu diesem Zeitpunkt das andere Objekt beeinflussen. Wenn das Universum jedoch zuließe, dass sich Objekte von verschiedenen Zeitpunkten aus gegenseitig beeinflussen, wären Zeitreisen nicht mehr notwendig. Da für die Rückwärtsverursachung keine Zeitreisen erforderlich sind, sind es im weiteren Sinne auch keine Kausalschleifen.
Kausalschleifen und mehrdimensionale Zeit
Die Struktur der Zeit mit Verzweigungen von Zeitlinien – manchmal auch als mehrdimensionale Zeit bezeichnet – beseitigt die meisten interessanten Merkmale von Kausalschleifen. (Siehe die Themenseite Mehrdimensionale Zeit auf unserer Website.) Tatsächlich wird sie manchmal eingeführt, um Kausalschleifen auszuschließen (Deutsch 1991, Deutsch und Lockwood 1994). Bei der mehrdimensionalen Zeit bewirkt das Zeitreisen eine Aufspaltung der Zeitlinien, so dass ein Ereignis kein Ereignis entlang seines eigenen Vergangenheitszweigs verursachen kann. Dadurch werden die Schleifen „ausgepackt“, und alles, was übrig bleibt, ist eine Reihe von geteilten Kausalketten. Eine Folge davon ist, dass die Antwort auf die Frage, ob Zeitreisen in die Vergangenheit immer eine Kausalschleife beinhalten, ein klares Nein wäre, wenn die mehrdimensionale Zeit wahr wäre. Ein Zeitreisender erzeugt Verzweigungen anstelle von Schleifen.
Kausalschleifen und Physik
Um einige theoretische Kausalschleifen in den Kontext der Physik einzuführen, lassen Sie uns die Idee einer zeitähnlichen Kurve betrachten. Eine zeitähnliche Kurve ist der Weg eines Objekts durch die Raumzeit, auf dem das Objekt lokal vorwärts in der Zeit verharrt, mit zeitähnlichen Verbindungen zwischen jedem Intervall. Eine kausale Schleife entsteht, wenn die zeitähnliche Kurve eines Objekts eine Schleife um sich selbst bildet.
Eine Möglichkeit, eine kausale Schleife einzuführen, ist die Vorstellung, dass das Universum eine aufgerollte Raumzeit hat (Gott 2001, 82-85). Die beste Analogie für diese Idee ist ein Zylinder, bei dem die Dimensionen, aus denen der Raum besteht, die Achsen des Zylinders sind. Diese Struktur ermöglicht es der zeitlichen Kurve eines Objekts, sich um den Zylinder zu wickeln und sich mit sich selbst zu treffen.
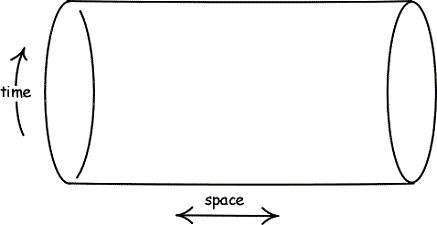
Abbildung 4: Gekrümmte Raum-Zeit
Wurmloch-basierte Zeitreisen ermöglichen ebenfalls geschlossene zeitliche Kurven, siehe die Themenseite Relativität und Zeitreisen auf unserer Website.
Die Physik stellt die Möglichkeit von Dschinns vor einige ernsthafte Probleme. Nach dem zweiten Hauptsatz der Thermodynamik nimmt die Entropie (oder Unordnung) immer mit der Zeit zu. Nehmen wir das Beispiel der Halskette in Timerider. Nach der Thermodynamik würde die Entropie der Halskette unter normalen Umständen von dem Moment an zunehmen, in dem Claire die Halskette stiehlt, bis zu dem Zeitpunkt, an dem die Halskette an Swann weitergegeben wird und bis Swann in die Vergangenheit reist. Nach den meisten Auffassungen von Zeitreisen ändert sich der Zustand von Objekten nicht, wenn sie in der Zeit zurückreisen. Da jedoch die Entropie der Halskette kurz vor Swanns Rückreise die gleiche Menge an Entropie aufweisen sollte wie bei Swanns Ankunft in der Vergangenheit, würde dies zu einem Widerspruch führen. Ein Widerspruch ergibt sich, weil die Entropie der Halskette kurz vor Swanns Abreise gleich und größer ist als die Entropie bei Swanns Ankunft in der Vergangenheit. Dieser Widerspruch bedeutet, dass Zeitreisemodelle für die Existenz von Dschinns in irgendeiner Weise für die Verringerung der Entropie bei ihrer Rückkehr in die Vergangenheit sorgen müssen (Gott 2001, 23).
Eine letzte interessante Anwendung von Kausalschleifen in der Physik ist die Hypothese, dass das Universum nicht aus einem Urknall hervorgegangen ist, sondern als ein Raum-Zeit-„Doughnut“ begann, aus dem sich der Rest des Universums verzweigte. Die Autoren dieser Theorie, J. Richard Gott und Li-Xin Li (Gott 2001, 186-199), formulierten diese Theorie auf der Grundlage einer alternativen Lösung der Einsteinschen Feldgleichungen. Der Raum-Zeit-Doughnut ist im Wesentlichen eine kausale Schleife mit sowohl geschlossenen als auch offenen Pfaden um die Schleife herum. Einige Pfade durch die Raumzeit existieren also als Schleife, aber es gibt andere, die sich verzweigen, um den Rest des Universums und seinen Inhalt zu bilden (vgl. Meyer 2012, 259).
Schlussfolgerung
Zurück zu dem Eingangsbeispiel über die moralisch zweideutige Hausarbeit, lassen Sie uns einen genaueren Blick darauf werfen. Wie Sie vielleicht schon erraten haben, können wir zwar einige Aspekte dieser Geschichte erfolgreich analysieren, aber viele interessante Fragen sind noch offen. Haben Sie zum Beispiel plagiiert, als Sie die Arbeit eingereicht haben? Sie haben sich nicht hingesetzt und die Arbeit geschrieben, aber Sie haben auch nicht kopiert oder sich gar auf die Arbeit anderer gestützt! Ein anderes Beispiel: Sind die Ideen in der Arbeit Dschinns? Sind die digitalen Informationen auf dem USB-Stick ein Dschinn? Ist das USB-Laufwerk selbst ein Dschinn? Ist die Geschichte mit der Thermodynamik vereinbar? Nichts in der Geschichte deutet darauf hin, dass die Entropie irgendwie nicht zunimmt, während der USB-Stick eine Woche lang in Ihrer Hose schmachtet. Trotz dieser offenen Fragen sind wir nicht auf ein inhärentes Paradoxon in Verbindung mit Kausalschleifen gestoßen.
Referenzen und weiterführende Literatur
Arntzenius, Frank und Maudlin, Tim. „Time Travel and Modern Physics“. The Stanford Encyclopedia of Philosophy (Winter 2013 Edition), Edward N. Zalta (ed.), <http://plato.stanford.edu/archives/win2013/entries/time-travel-phys/>.
Dear, William. (director). Timerider: The Adventures of Lynn Swann . USA: Zoomo Productions, 1982.
Deutsch, David. ‚Quantum Mechanics Near Closed Timelike Lines.‘ Physical Review D 44 (1991): 3197-3217.
Deutsch, David, und Lockwood, Michael. ‚The Quantum Physics of Time Travel.‘ Scientific American 270 (1990): 68-74.
Gott, J. Richard. Time Travel in Einstein’s Universe. Boston: Houghton-Mifflin, 2001.
McCall, Storrs. „An Insoluble Problem.“ Analysis 70 (2010): 647-648.
Mellor, D. H. Real Time. London: Routledge, 1998.
Meyer, Ulrich. „Explaining Causal Loops.“ Analysis 72 (2012): 259-264.
Monton, Bradley. „Time Travel without Causal Loops.“ The Philosophical Quarterly 59 (2009): 54-67.
Für den Seitenabspann siehe die Seite „Themen-Seitenabspann“.