Der Winkel, der entsteht, wenn der Radius
um den Kreis gewickelt wird:
 |
1 Bogenmaß ist etwa 57,2958 Grad. |
Warum „57,2958…“ Grad? Das werden wir gleich sehen.
Der Radiant ist ein reines Maß, das auf dem Radius des Kreises basiert:
Radiant: der Winkel, der entsteht, wenn wir den Radius
nehmen und ihn um den Kreis wickeln.
Radian und Grad
Lassen Sie uns sehen, warum 1 Radian gleich 57.2958… Grad:
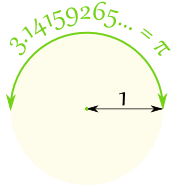
In einem Halbkreis gibt esπ Bogenmaß, das auch 180° ist
Um von Bogenmaß zu Grad zu kommen: mit 180 multiplizieren, durch π dividieren
Um von Grad zu Bogenmaß zu kommen: mit π multiplizieren, durch 180 dividieren
Hier ist eine Tabelle mit entsprechenden Werten:
| Grad | Bogenmaß (genau) |
Bogenmaß (ungefähr) |
|---|---|---|
| 30° | π/6 | 0.524 |
| 45° | π/4 | 0.785 |
| 60° | π/3 | 1.047 |
| 90° | π/2 | 1.571 |
| 180° | π | 3.142 |
| 270° | 3π/2 | 4.712 |
| 360° | 2π | 6.283 |
Beispiel: Wie viele Radien hat ein Vollkreis?
Stellen Sie sich vor, Sie schneiden ein Stück Schnur ab, das genau die Länge vom Mittelpunkt bis zum Umfang eines Kreises hat …
… wie viele Stücke brauchst du, um einmal um den Kreis zu gehen?
Antwort: 2π (oder etwa 6,283 Stücke Schnur).
Von Mathematikern bevorzugte Radien
Da der Bogenmaß auf der reinen Vorstellung beruht, dass „der Radius entlang des Umfangs gelegt wird“, liefert er oft einfache und natürliche Ergebnisse, wenn er in der Mathematik verwendet wird.
Betrachten Sie zum Beispiel die Sinusfunktion für sehr kleine Werte:

