Es kommt nicht oft vor, dass eine mathematische Gleichung es in die nationale Presse schafft, geschweige denn ins Radio, oder, was am erstaunlichsten ist, Gegenstand einer Debatte im britischen Parlament ist. Im Jahr 2003 jedoch war die gute alte quadratische Gleichung, die wir alle in der Schule gelernt haben, all das.
Wo wir beginnen

Alles begann bei einer Sitzung der National Union of Teachers. Die quadratische Gleichung wurde der Nation als Beispiel für die grausame Folter vorgeführt, die Mathematiker armen, ahnungslosen Schulkindern zufügen. Unter dem Eindruck dieser Anschuldigung erhielt die quadratische Gleichung eine Hauptrolle in einer Radiosendung zur besten Sendezeit, wo sie von einem furchteinflößenden Interviewer befragt wurde, der es sonst eher mit dem Premierminister aufnimmt. Die (Londoner) Times nahm in ihrer Leitartikelspalte, die normalerweise für gewichtige Diskussionen über den moralischen Zustand der modernen Welt reserviert ist, Platz, um zu verkünden, dass die quadratische Gleichung nutzlos sei, dass Mathematik nutzlos sei und dass sowieso niemand Mathematik studieren wolle, warum also die Mühe. Aus Sorge, dass die gefährlichen Eingeständnisse der quadratischen Gleichung unwidersprochen bleiben könnten, wurde im britischen Unterhaus über die lebenswichtige Bedeutung der Gleichung für das Überleben des Vereinigten Königreichs debattiert (mit einem positiven Ergebnis, wie Sie vielleicht wissen).
Wo würde das alles enden? War die quadratische Gleichung wirklich tot? War sie jemandem egal? Sind Mathematiker wirklich böse Monster, die einer jüngeren Generation quadratische Gleichungen aufzwingen wollen, um ihre unsterblichen Seelen zu verderben?
Vielleicht ja, aber es ist nicht wirklich die Schuld der quadratischen Gleichung. Tatsächlich hat die quadratische Gleichung nicht nur für die gesamte menschliche Zivilisation, wie wir sie kennen, eine entscheidende Rolle gespielt, sondern auch für die mögliche Entdeckung anderer außerirdischer Zivilisationen und sogar für so wichtige moderne Aktivitäten wie Satellitenfernsehen. Was sonst, abgesehen von der Natur der göttlichen Offenbarung, könnte einen solchen Einfluss auf das Leben, wie wir es kennen, haben? In der Tat können quadratische Gleichungen im wahrsten Sinne des Wortes Ihr Leben retten.
Die Babylonier
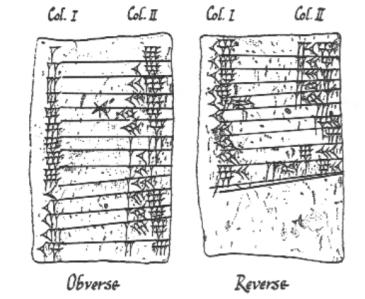
Babylonische Keilschrifttafeln, auf denen die 9 Zeittafeln aufgezeichnet sind
Alles begann um 3000 v. Chr. mit den Babyloniern. Sie waren eine der ersten Zivilisationen der Welt und hatten einige großartige Ideen wie Landwirtschaft, Bewässerung und Schrift. Sie zeichneten die Bahnen der Sonne, des Mondes und der Planeten auf und hielten sie auf Tontafeln fest (die man heute noch im Britischen Museum sehen kann). Den Babyloniern verdanken wir die modernen Vorstellungen von Winkeln, einschließlich der Art und Weise, wie der Kreis in 360 Grad aufgeteilt ist (aufgrund eines kleinen Rechenfehlers, einer pro Tag). Den Babyloniern verdanken wir auch die etwas weniger angenehme Erfindung des (gefürchteten) Steuereintreibers. Und das war einer der Gründe, warum die Babylonier quadratische Gleichungen lösen mussten.
Stellen Sie sich vor, Sie sind ein babylonischer Bauer. Irgendwo auf Ihrem Hof haben Sie ein quadratisches Feld, auf dem Sie etwas anbauen. Wie viel von deiner Ernte kannst du auf dem Feld anbauen? Verdoppeln Sie die Länge jeder Seite des Feldes, und Sie werden feststellen, dass Sie viermal so viel anbauen können wie vorher. Der Grund dafür ist, dass die Menge der Ernte, die Sie anbauen können, proportional zur Fläche des Feldes ist, die wiederum proportional zum Quadrat der Länge der Seite ist. Mathematisch ausgedrückt: Wenn  die Seitenlänge des Feldes ist,
die Seitenlänge des Feldes ist, 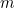 die Menge der Ernte, die man auf einem quadratischen Feld der Seitenlänge 1 anbauen kann, und
die Menge der Ernte, die man auf einem quadratischen Feld der Seitenlänge 1 anbauen kann, und  die Menge der Ernte, die man anbauen kann, dann
die Menge der Ernte, die man anbauen kann, dann
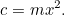 |
Dies ist unsere erste quadratische Gleichung, die nackt im Sonnenlicht blinkt. Quadratische Gleichungen und Flächen sind wie Brüder und Schwestern in einer Familie miteinander verbunden. Aber im Moment müssen wir noch nichts lösen – bis der Finanzbeamte kommt! Fröhlich sagt er zu dem Bauern: „Ich möchte, dass du mir Ernten gibst, um die Steuern für deinen Hof zu bezahlen.“ Der Bauer steht nun vor einem Dilemma: Wie groß muss sein Feld sein, um diese Menge an Getreide anzubauen? Wir können diese Frage leicht beantworten, denn
Ernten gibst, um die Steuern für deinen Hof zu bezahlen.“ Der Bauer steht nun vor einem Dilemma: Wie groß muss sein Feld sein, um diese Menge an Getreide anzubauen? Wir können diese Frage leicht beantworten, denn
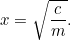 |
Das Finden von Quadratwurzeln mit Hilfe eines Taschenrechners ist für uns einfach, war aber für die Babylonier ein größeres Problem. Sie entwickelten nämlich eine Methode der sukzessiven Annäherung an die Antwort, die identisch ist mit dem Algorithmus (genannt Newton-Raphson-Methode), der von modernen Computern verwendet wird, um viel schwierigere Probleme als quadratische Gleichungen zu lösen.
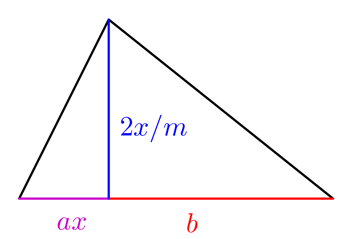
Nun sind aber nicht alle Felder quadratisch. Nehmen wir nun an, dass der Landwirt ein eher ungerade geformtes Feld mit zwei dreieckigen Abschnitten hat, wie rechts dargestellt.
Für geeignete Werte von  und
und 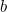 ist die Erntemenge, die der Bauer auf diesem Feld anbauen kann, gegeben durch
ist die Erntemenge, die der Bauer auf diesem Feld anbauen kann, gegeben durch
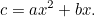 |
Das sieht viel mehr nach der quadratischen Gleichung aus, an die wir gewöhnt sind, und selbst unter dem bösen Blick des Steuerbeamten ist sie viel schwieriger zu lösen. Doch die Babylonier haben die Lösung wieder gefunden. Zuerst dividieren wir durch  und erhalten
und erhalten
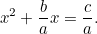 |
Nun vervollständigen wir das Quadrat, indem wir die Tatsache nutzen, dass
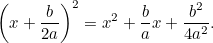 |
Kombiniert man dies mit der ursprünglichen Gleichung, erhält man
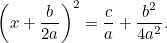 |
Dies ist nun eine Gleichung, die man durch Ziehen der Quadratwurzeln lösen kann. Das Ergebnis ist die berühmte „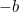 -Formel“:
-Formel“:
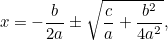 |
, die umgeschrieben werden kann als
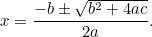 |
(Die Formel hat normalerweise „-4ac“, weil die quadratische Gleichung üblicherweise in der Form „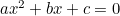 “ geschrieben wird.)
“ geschrieben wird.)
Die Tatsache, dass das Ziehen einer Quadratwurzel eine positive oder negative Antwort ergeben kann, führt zu dem bemerkenswerten Ergebnis, dass eine quadratische Gleichung zwei Lösungen hat. So viel zu mathematischen Rätseln, die nur eine Lösung haben!
Nun, hier hört der Unterricht über quadratische Gleichungen oft auf. Wir sind bei dem Objekt angelangt, das von allen Journalisten geliebt wird, wenn sie Mathematiker interviewen – eine Formel. Man kann sich endlose Fragen ausdenken, bei denen es darum geht, Werte von 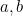 und
und  in die Formel einzusetzen, um (zwei) Antworten zu erhalten. Aber darum geht es in der Mathematik überhaupt nicht. Eine Formel zu finden, ist nur der erste Schritt auf einem langen Weg. Wir müssen uns fragen, was die Formel bedeutet, was sie uns über das Universum verrät und ob es wirklich wichtig ist, eine Formel zu haben. Mal sehen, wohin uns diese Formel führen wird.
in die Formel einzusetzen, um (zwei) Antworten zu erhalten. Aber darum geht es in der Mathematik überhaupt nicht. Eine Formel zu finden, ist nur der erste Schritt auf einem langen Weg. Wir müssen uns fragen, was die Formel bedeutet, was sie uns über das Universum verrät und ob es wirklich wichtig ist, eine Formel zu haben. Mal sehen, wohin uns diese Formel führen wird.
Eine Überraschung für die Griechen, ein bisschen mathematisches Origami und ein Sinn für Proportionen
Wir spulen nun 1000 Jahre vor bis zu den alten Griechen und sehen, was sie aus quadratischen Gleichungen machten. Die Griechen waren hervorragende Mathematiker und entdeckten einen Großteil der Mathematik, die wir heute noch verwenden. Eine der Gleichungen, die sie lösen wollten, war die (einfache) quadratische Gleichung
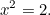 |

Sie wussten, dass diese Gleichung eine Lösung hat. Es handelt sich nämlich um die Länge der Hypotenuse eines rechtwinkligen Dreiecks, dessen Seiten die Länge eins haben.
Aus dem Satz des Pythagoras folgt, dass, wenn ein rechtwinkligesrechtwinkliges Dreieck die kürzeren Seiten  und
und  und die Hypotenuse
und die Hypotenuse  hat, dann
hat, dann
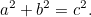 |
Setzt man 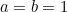 und
und  dann
dann 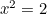 . Also
. Also 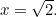
Was ist also  in diesem Fall? Oder, um die Frage zu stellen, die die Griechen gestellt haben, was für eine Zahl ist das? Der Grund dafür, dass dies wichtig war, lag im Verhältnismäßigkeitssinn der Griechen. Sie glaubten, dass alle Zahlen in einem bestimmten Verhältnis zueinander stehen. Genauer gesagt bedeutete dies, dass alle Zahlen Brüche der Form
in diesem Fall? Oder, um die Frage zu stellen, die die Griechen gestellt haben, was für eine Zahl ist das? Der Grund dafür, dass dies wichtig war, lag im Verhältnismäßigkeitssinn der Griechen. Sie glaubten, dass alle Zahlen in einem bestimmten Verhältnis zueinander stehen. Genauer gesagt bedeutete dies, dass alle Zahlen Brüche der Form 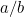 waren, wobei
waren, wobei  und
und  ganze Zahlen sind. Zahlen wie 1/2, 3/4 und 355/113 sind alles Beispiele für Brüche. Es war naheliegend zu erwarten, dass
ganze Zahlen sind. Zahlen wie 1/2, 3/4 und 355/113 sind alles Beispiele für Brüche. Es war naheliegend zu erwarten, dass  auch ein Bruch ist. Die große Überraschung war, dass dies nicht der Fall ist. Tatsächlich ist
auch ein Bruch ist. Die große Überraschung war, dass dies nicht der Fall ist. Tatsächlich ist
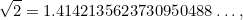 |
, wobei die Punkte  bedeuten, dass die dezimale Erweiterung von
bedeuten, dass die dezimale Erweiterung von  ohne erkennbares Muster bis ins Unendliche geht. (
ohne erkennbares Muster bis ins Unendliche geht. (
 war die erste irrationale Zahl (d. h. eine Zahl, die weder ein Bruch noch rational ist), die als solche anerkannt wurde. Andere Beispiele sind
war die erste irrationale Zahl (d. h. eine Zahl, die weder ein Bruch noch rational ist), die als solche anerkannt wurde. Andere Beispiele sind 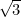 ,
, 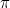 ,
,  und eigentlich „die meisten“ Zahlen. Es dauerte bis zum 19. Jahrhundert, bis wir eine gute Möglichkeit hatten, über diese Zahlen nachzudenken. Die Entdeckung, dass
und eigentlich „die meisten“ Zahlen. Es dauerte bis zum 19. Jahrhundert, bis wir eine gute Möglichkeit hatten, über diese Zahlen nachzudenken. Die Entdeckung, dass  keine rationale Zahl war, löste sowohl große Aufregung (100 Ochsen wurden dafür geopfert) als auch einen großen Schock aus, da der Entdecker Selbstmord begehen musste. (Möge dies eine schreckliche Warnung für die mathematisch Interessierten sein!) Zu diesem Zeitpunkt gaben die Griechen die Algebra auf und wandten sich der Geometrie zu.
keine rationale Zahl war, löste sowohl große Aufregung (100 Ochsen wurden dafür geopfert) als auch einen großen Schock aus, da der Entdecker Selbstmord begehen musste. (Möge dies eine schreckliche Warnung für die mathematisch Interessierten sein!) Zu diesem Zeitpunkt gaben die Griechen die Algebra auf und wandten sich der Geometrie zu.
Die  ist keineswegs eine obskure Zahl, sondern begegnet uns regelmäßig: immer dann, wenn wir ein Stück A4-Papier benutzen. In Europa werden die Papierformate in A-Formaten gemessen, wobei A0 das größte Format mit einer Fläche von
ist keineswegs eine obskure Zahl, sondern begegnet uns regelmäßig: immer dann, wenn wir ein Stück A4-Papier benutzen. In Europa werden die Papierformate in A-Formaten gemessen, wobei A0 das größte Format mit einer Fläche von 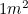 ist. Die A-Formate stehen in einem besonderen Verhältnis zueinander. Wenn wir nun ein wenig Origami machen, indem wir ein Blatt A1-Papier nehmen und es in der Mitte (entlang der längsten Seite) falten, erhalten wir A2-Papier. Faltet man es noch einmal in der Hälfte, erhält man A3, und noch einmal A4 usw. Das Papier ist jedoch so beschaffen, dass die Proportionen der einzelnen A-Größen gleich sind – das heißt, jedes Stück Papier hat die gleiche Form.
ist. Die A-Formate stehen in einem besonderen Verhältnis zueinander. Wenn wir nun ein wenig Origami machen, indem wir ein Blatt A1-Papier nehmen und es in der Mitte (entlang der längsten Seite) falten, erhalten wir A2-Papier. Faltet man es noch einmal in der Hälfte, erhält man A3, und noch einmal A4 usw. Das Papier ist jedoch so beschaffen, dass die Proportionen der einzelnen A-Größen gleich sind – das heißt, jedes Stück Papier hat die gleiche Form.
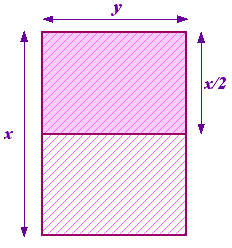
Wir können uns die Frage stellen, welche Proportion das ist. Beginne mit einem Stück Papier mit den Seiten x und y, wobei x die längste Seite ist. Nun teilen wir es durch zwei und erhalten ein weiteres Stück Papier mit den Seiten y und x/2, wobei nun y die längste Seite ist. Dies ist auf der rechten Seite dargestellt.
Die Proportionen des ersten Stücks Papier sind 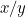 und die des zweiten
und die des zweiten 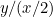 oder
oder 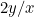 . Wir wollen, dass diese beiden Proportionen gleich sind. Das bedeutet, dass
. Wir wollen, dass diese beiden Proportionen gleich sind. Das bedeutet, dass
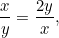 |
oder
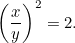 |
Eine weitere quadratische Gleichung! Zum Glück ist es eine, die wir schon kennen. Wenn wir sie lösen, stellen wir fest, dass
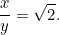 |
Dieses Ergebnis lässt sich leicht überprüfen. Nehmen Sie einfach ein Blatt Papier im Format A4 (oder A3 oder A5) und messen Sie die Seiten. Wir können auch die Größe der einzelnen Blätter berechnen. Der Flächeninhalt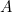 eines Blattes A0 ist gegeben durch
eines Blattes A0 ist gegeben durch
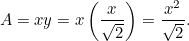 |
Aber wir wissen, dass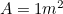 , also haben wir eine weitere quadratische Gleichung für die längste Seite
, also haben wir eine weitere quadratische Gleichung für die längste Seite von A0, gegeben durch
von A0, gegeben durch
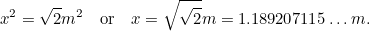 |
Das bedeutet, dass die längste Seite von A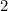 gegeben ist durch
gegeben ist durch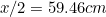 (warum?) und die von A
(warum?) und die von A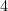 durch
durch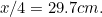 . Überprüfe dies auf deinem eigenen Blatt Papier.
. Überprüfe dies auf deinem eigenen Blatt Papier.
Das in den Vereinigten Staaten verwendete Papier, Foolscap genannt, hat ein anderes Verhältnis. Um zu sehen, warum, kehren wir zu den Griechen und einer anderen quadratischen Gleichung zurück. Die quadratische Gleichung, die so viel Kummer verursacht hat, hat sich bei der Suche nach den perfekten Proportionen bewährt: eine Suche, die bis heute bei der Gestaltung von Filmkulissen fortgesetzt wird und in vielen Aspekten der Natur zu beobachten ist.
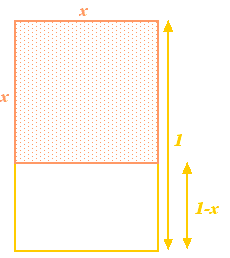
Beginnen wir mit einem Rechteck und entfernen wir daraus ein Quadrat mit der gleichen Seitenlänge wie die kürzeste Seite des Rechtecks. Wenn die längste Seite des Rechtecks die Länge 1 und die kürzeste Seite die Länge  hat, dann hat das Quadrat Seiten der Länge
hat, dann hat das Quadrat Seiten der Länge  . Entfernt man es aus dem Rechteck, entsteht ein kleineres Rechteck mit der längsten Seite
. Entfernt man es aus dem Rechteck, entsteht ein kleineres Rechteck mit der längsten Seite  und der kleinsten Seite
und der kleinsten Seite 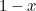 . So weit, so abstrakt. Die Griechen glaubten jedoch, dass das Rechteck mit den ästhetischsten Proportionen (das so genannte Goldene Rechteck) dasjenige ist, bei dem das große und das kleine, oben konstruierte Rechteck die gleichen Proportionen haben. Damit dies möglich ist, müssen wir
. So weit, so abstrakt. Die Griechen glaubten jedoch, dass das Rechteck mit den ästhetischsten Proportionen (das so genannte Goldene Rechteck) dasjenige ist, bei dem das große und das kleine, oben konstruierte Rechteck die gleichen Proportionen haben. Damit dies möglich ist, müssen wir
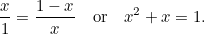 |
Dies ist eine weitere quadratische Gleichung: eine sehr wichtige Gleichung, die in allen möglichen Anwendungen auftaucht. Sie hat die (positive) Lösung
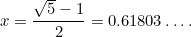 |
Die Zahl  wird als Goldener Schnitt bezeichnet und wird oft mit dem griechischen Buchstaben
wird als Goldener Schnitt bezeichnet und wird oft mit dem griechischen Buchstaben 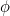 bezeichnet.
bezeichnet.

Das Goldene Rechteck ist in der Form von Fenstern zu sehen, insbesondere an georgianischen Häusern. In jüngerer Zeit findet man den Goldenen Schnitt auch als „perfekte Form“ für Fotos und Filmbilder. Die quadratische Gleichung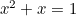 taucht auch in Studien über die Populationen von Kaninchen und in dem Muster auf, in dem die Samen von Sonnenblumen und die Blätter an den Stängeln von Pflanzen angeordnet sind. Diese sind alle mit dem Goldenen Schnitt durch die Fibonacci-Folge verbunden, die durch
taucht auch in Studien über die Populationen von Kaninchen und in dem Muster auf, in dem die Samen von Sonnenblumen und die Blätter an den Stängeln von Pflanzen angeordnet sind. Diese sind alle mit dem Goldenen Schnitt durch die Fibonacci-Folge verbunden, die durch
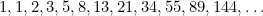 |

Sonnenblumensamen gegeben ist, angeordnet nach den Fibonacci-Zahlen |
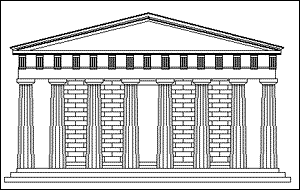
Der Parthenon, der den Goldenen Schnitt verkörpert |
In dieser Folge ist jeder Term die Summe der beiden vorhergehenden Terme. Fibonacci entdeckte ihn im 15. Jahrhundert, als er versuchte, die zukünftige Population von Kaninchen vorherzusagen. Nimmt man das Verhältnis jedes Terms zum nächsten, erhält man die Zahlenfolge
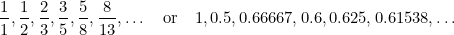 |
und diese Zahlen kommen dem Goldenen Schnitt 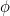 immer näher.
immer näher.
Wenn wir die beiden Wurzeln der obigen quadratischen Gleichung finden, können wir tatsächlich eine Formel für den n-ten Term in der Fibonacci-Folge finden. Wenn  die
die 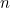 -te solche Zahl mit
-te solche Zahl mit 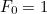 und
und 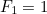 ist, dann ist
ist, dann ist  durch die Formel
durch die Formel
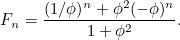 |
Konik verbindet quadratische Gleichungen mit den Sternen

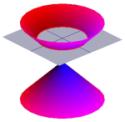
Auch die Griechen waren sehr an der Form von Kegeln interessiert. Das Bild links zeigt einen typischen Kegel.
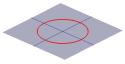
Die Hälfte des Kegels kann man sich als die Ausbreitung des Lichts einer Fackel vorstellen. Wenn man nun mit einer Taschenlampe auf eine flache Oberfläche, wie z. B. eine Wand, leuchtet, sieht man verschiedene Formen, wenn man die Taschenlampe hin und her bewegt. Diese Formen werden Kegelschnitte genannt und sind die Kurven, die man erhält, wenn man einen Kegel in verschiedenen Winkeln durchschneidet. Genau diese Kurven wurden von den Griechen untersucht, und sie erkannten, dass es grundsätzlich vier Arten von Kegelschnitten gibt. Wenn man einen horizontalen Schnitt durch den Kegel macht, erhält man einen Kreis. Ein Schnitt in einem kleinen Winkel zur Horizontalen ergibt eine Ellipse. Nimmt man einen vertikalen Schnitt, erhält man eine Hyperbel, und wenn man einen Schnitt parallel zu einer Seite des Kegels nimmt, erhält man eine Parabel. Diese Kurven sind im Folgenden dargestellt.
 |
 |
 |
 |
 |
 |
 |
 |

Ein Quer-Querschnitt eines Kegels kann ein Kreis sein … |

… eine Ellipse … |
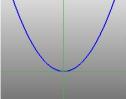
… eine Parabel … |
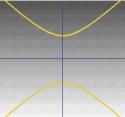
…. oder eine Hyperbel. |
Konische Schnitte kommen in unsere Geschichte, weil jeder von ihnen durch eine quadratische Gleichung beschrieben wird. Insbesondere, wenn 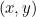 einen Punkt auf jeder Kurve darstellt, dann verbindet eine quadratische Gleichung
einen Punkt auf jeder Kurve darstellt, dann verbindet eine quadratische Gleichung  und
und 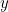 . Wir haben:
. Wir haben:
Der Kreis: 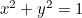 ;
;
Die Ellipse: 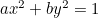 ;
;
Die Hyperbel: 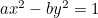 ;
;
Die Parabel: 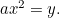
Diese Kurven waren seit den Griechen bekannt und wurden studiert, aber abgesehen vom Kreis schienen sie keine praktische Anwendung zu haben. Wie wir jedoch in der nächsten Ausgabe von Plus sehen werden, führte eine Verbindung zwischen quadratischen Gleichungen und Kegelschnitten, gepaart mit einem mächtigen Glücksfall, zu einem Verständnis der Funktionsweise des Universums, und im 16. Jahrhundert war die Zeit gekommen, als Kegelschnitte die Welt veränderten.
Über die Autoren
Chris Budd ist Professor für angewandte Mathematik in der Abteilung für mathematische Wissenschaften an der Universität Bath und Inhaber des Lehrstuhls für Mathematik an der Royal Institution in London.
Chris Sangwin ist Mitarbeiter der School of Mathematics and Statistics an der Universität Birmingham. Er ist Research Fellow im Learning and Teaching Support Network Centre for Mathematics, Statistics, and Operational Research.
Sie haben kürzlich das populäre Mathematikbuch Mathematics Galore! geschrieben, das von Oxford University Press veröffentlicht wurde.
Dieser Artikel wurde zum Teil durch eine bemerkenswerte Debatte im britischen Unterhaus zum Thema quadratische Gleichungen inspiriert. Das Protokoll dieser Debatte findet sich im Hansard, United Kingdom House of Commons, 26. Juni 2003, Spalten 1259-1269, 2003, das online auf der House of Commons Hansard Debate Website verfügbar ist.